题目内容
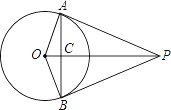
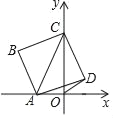
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标;
(2)若折叠后点B落在边OA上的点为B′,设OB′=x,OC=y,试写出y关于x的函数解析式,并确定y的取值范围;
(3)若折叠后点B落在边OA上的点为B′,且使B′D//OB,求此时点C的坐标.

【答案】(1) C(0,![]() );(2)y=﹣
);(2)y=﹣![]() x2+2,y的取值范围是
x2+2,y的取值范围是![]() ≤y≤2. (3)C的坐标是(0,﹣16+8
≤y≤2. (3)C的坐标是(0,﹣16+8![]() )
)
【解析】
(1)因为折叠后点B与点A重合,那么BC=AC,可先设出C点的坐标,然后表示出BC,AC,在直角三角形OCA中,根据勾股定理即可求出C点的纵坐标,也就求出了C点的坐标;
(2)方法同(1)用OC表示出BC,B′C然后在直角三角形OB′C中根据勾股定理得出x,y的关系式.由于B′在OA上,因此有0≤x≤2,由此可求出y的取值范围;
(3)根据(1)(2)的思路,应该先得出OB″,OC的关系,知道OA,OB的值,那么可以通过证Rt△COB″∽Rt△BOA来实现.∠B″CO和∠CB″D是平行线B″D,OB的内错角,又因为∠OBA=∠CB″D,因此∠B″CO=∠OBA,即CB″∥BA,由此可得出两三角形相似,得出OC,OB″的比例关系,然后根据(1)(2)的思路,在直角三角形OB″C中求出OC的值,也就求出C点的坐标了.
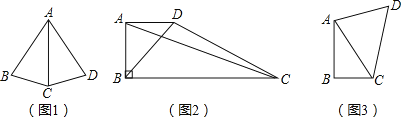
(1)如图①,折叠后点B与点A重合,则△ACD≌△BCD.
设点C的坐标为(0,m)(m>0),则BC=OB-OC=4-m.
∴AC=BC=4-m.
在Rt△AOC中,由勾股定理,AC2=OC2+OA2,
即(4-m)2=m2+22,解得m=![]() .
.
∴点C的坐标为(0,![]() );
);

(2)如图②,折叠后点B落在OA边上的点为B′,
∴△B′CD≌△BCD.
∵OB′=x,OC=y,
∴B′C=BC=OB-OC=4-y,
在Rt△B′OC中,由勾股定理,得B′C2=OC2+OB′2.
∴(4-y)2=y2+x2,
即y=-![]() x2+2.
x2+2.
由点B′在边OA上,有0≤x≤2,
∴解析式y=-![]() x2+2(0≤x≤2)为所求.
x2+2(0≤x≤2)为所求.
∵当0≤x≤2时,y随x的增大而减小,
∴y的取值范围为![]() ≤y≤2;
≤y≤2;
(3)如图③,折叠后点B落在OA边上的点为B″,且B″D∥OC.
∴∠OCB″=∠CB″D.
又∵∠CBD=∠CB″D,
∴∠OCB″=∠CBD,
∵CB″∥BA.
∴Rt△COB″∽Rt△BOA.
∴![]() ,
,
∴OC=2OB″.
在Rt△B″OC中,
设OB″=x0(x0>0),则OC=2x0.
由(2)的结论,得2x0=-![]() x02+2,
x02+2,
解得x0=-8±4![]() .
.
∵x0>0,
∴x0=-8+4![]() .
.
∴点C的坐标为(0,-16+8![]() ).
).

 备战中考寒假系列答案
备战中考寒假系列答案