Question

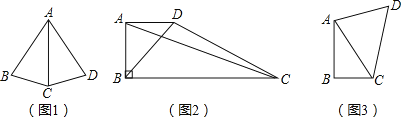
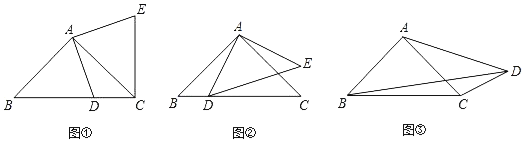
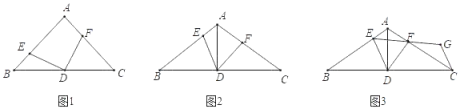
【题目】在△ABC中，AB＝AC，点D是BC中点，∠EDF两边分别交线段AB于点E，交线段AC于点F，且∠EDF+∠BAC＝180°

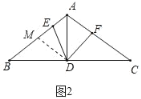
（1）如图1，当∠EDF＝90°时，求证：BE＝AF；

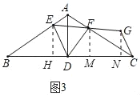
（2）如图2，当∠EDF＝60°时，求证：AE+AF＝AD；

（3）如图3，在（2）的条件下，连接EF并延长EF至点G，使FG＝EF，连接CG，若BE＝5，CF＝4，求CG的长度．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）CG＝．

【解析】

1）由等腰三角形的性质得出AD⊥BC，AD＝BC＝BD＝CD，∠B＝∠C＝45°，∠DAF＝∠BAC＝45°，求出∠B＝∠DAF，∠BDE＝∠ADF，由ASA证明△BDE≌△ADF，即可得出结论；

（2）取AB的中点M，连接DM，由直角三角形的性质得出DM＝AB＝BM＝AM，证出△ADM是等边三角形，得出AM＝DM＝AD，∠AMD＝∠ADM＝60°，证明△DEM≌△DFA，得出MD＝AF，即可得出结论；

（3）作EH⊥BC于H，FM⊥BC于M，GN⊥BC于N，则EH∥FM∥GN，由（2）得：AE＋AF＝AD，由等腰三角形的性质得出∠B＝∠ACB＝30°，AD⊥BC，∠ADB＝∠ADC＝90°，由直角三角形的性质得出AD＝AB，BD＝CD＝AD，EH＝BE＝，FM＝CF＝2，BH＝EH＝，CM＝FM＝2，求出AB＝6，得出AD＝3，BD＝CD＝3，∴DH＝BDBH＝，DM＝CDCM＝，求出HM＝DH＋DM＝，证出FM是梯形EHNG的中位线，HM＝MN，得出2FM＝EH＋GN，MN＝，CN＝CDDMMN＝，求出GN＝，在Rt△CGN中，由勾股定理即可求出CG的长．

（1）证明：连接AD，如图1所示：

∵∠EDF+∠BAC＝180°，∠EDF＝90°，

∴∠BAC＝90°，

∵AB＝AC，点D是BC中点，

∴AD⊥BC，AD＝BC＝BD＝CD，∠B＝∠C＝45°，∠DAF＝∠BAC＝45°，

∴∠B＝∠DAF，

∵∠EDF＝90°，

∴∠BDE＝∠ADF，

在△BDE和△ADF中，，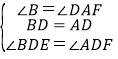

∴△BDE≌△ADF（ASA），

∴BE＝AF；

（2）证明：取AB的中点M，连接DM，如图2所示：

∵AD⊥BC，M是AB的中点，

∴DM＝AB＝BM＝AM，

∵∠EDF+∠BAC＝180°，∠EDF＝60°，

∴∠BAC＝120°，

∵AB＝AC，点D是BC中点，

∴∠BAD＝∠CAD＝∠BAC＝60°，

∴△ADM是等边三角形，

∴AM＝DM＝AD，∠AMD＝∠ADM＝60°，

∴∠MDE＝∠ADF，

在△DEM和△DFA中，，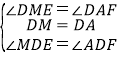

∴△DEM≌△DFA（ASA），

∴MD＝AF，

∵AE+ME＝AM＝AD，

∴AE+AF＝AD；

（3）解：作EH⊥BC于H，FM⊥BC于M，GN⊥BC于N，如图3所示：

则EH∥FM∥GN，

由（2）得：AE+AF＝AD，

∵BE＝5，CF＝4，AB+AC＝BE+AE+AF+CF＝BE+AD+CF＝5+AD+4＝9+AD，

∵∠BAC＝120°，AB＝AC，点D是BC中点，

∴∠B＝∠ACB＝30°，AD⊥BC，∠ADB＝∠ADC＝90°，

∴AD＝AB，BD＝CD＝AD，EH＝BE＝，FM＝CF＝2，BH＝EH＝，CM＝FM＝2，

∴2AB＝9+AB，

解得：AB＝6，

∴AD＝3，BD＝CD＝3，

∴DH＝BD﹣BH＝，DM＝CD﹣CM＝，

∴HM＝DH+DM＝，

∵EH∥FM∥GN，EF＝FG，

∴FM是梯形EHNG的中位线，HM＝MN，

∴2FM＝EH+GN，MN＝，CN＝CD﹣DM﹣MN＝3﹣﹣＝，2×2＝+GN，

∴GN＝，

在Rt△CGN中，由勾股定理得：CG＝=．