Question

【题目】如图，△ABC中，AB=AC=15，∠BAC=120°，小明要将该三角形分割成两个直角三角形和两个等腰三角形，他想出了如下方案：在AB上取点D，过点D画DE∥AC交BC于点E，连结AE，在AC上取合适的点F，连结EF可得到4个符合条件的三角形，则满足条件的AF长是______．

Answer 1

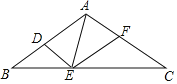
【答案】7.5

【解析】

根据已知条件可判定△BDE和△EFC始终为等腰三角形，并可求得∠AFE=∠ADE=30°，若△AEF和△ADE为等腰三角形，则必为等边三角形．将求AF的长度转化为求AE的长度．然后通过解Rt△AEC即可．也可以用直角三角形斜边上的中线等于斜边的一半求解．

解：如图

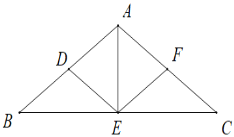
∵AB=AC

∴∠B=∠C

∵∠BAC=120°，∠BAC+∠B+∠C=180°

∴∠B=∠C=30°

∵DE∥∥AC，EF∥AB

∴∠DEB=∠C=30°，∠FEC=∠B=30°

∴∠B=∠DEB，∠C=∠FEC

∴△DBE，△FEC是等腰三角形

∵AB∥EF

∴∠EFA+∠BAC=180

∴∠EFA=60°

∵△AEF是等腰三角形

∴△AEF是等边三角形

∴AF=AE，∠AEF=∠EFA=60°

∴∠AEC=∠AEF+∠FEC=90°

在Rt△AEC中，AC=15，∠C=30°，∠AEC=90°

∴AF=7.5

故答案为7.5