Question

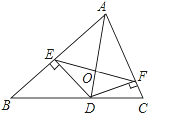
【题目】如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE,则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是 （　　）

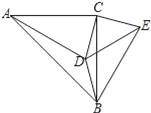
A. ①②③ B. ①②④ C. ①③④ D. ①②③④

Answer 1

【答案】D

【解析】

①根据：∠CAD=30°，AC=BC=AD，利用等腰三角形的性质和三角形内角和定理即可求出∠ECA=165°，从而得证结论正确；②根据CE⊥CD，∠ECA=165°，利用SAS求证△ACD≌△BCE即可得出结论；③由②的结论，等量代换即可；④过D作DM⊥AC于M，过D作DN⊥BC于N．由∠CAD=30°，可得CM=AC，求证△CMD≌△CND，可得CN=DM=AC=BC，从而得出CN=BN．然后即可得出结论．

∵∠CAD=30°，AC=AD，

∴∠ACD=∠ADC=75°，

∵CE⊥CD，

∴∠ECA=165°，①正确；

∵∠ACB=∠DCE=90°，

∴∠ACD=∠BCE，

在△ACD和△BCE中，

，

∴△ACD≌△BCE，

∴BE=AD，③正确；

∵BC=AD，

∴BE=BC，②正确；

过D作DM⊥AC于M，过D作DN⊥BC于N．

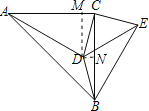
∵∠CAD=30°，且DM=AC，

∵AC=AD，∠CAD=30°，

∴∠ACD=75°，

∴∠NCD=90°-∠ACD=15°，∠MDC=∠DMC-∠ACD=15°，

在△CMD和△CND中，，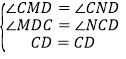

∴△CMD≌△CND，

∴CN=DM=AC=BC，

∴CN=BN．

∵DN⊥BC，

∴BD=CD．

∴④正确，

故选D．