题目内容
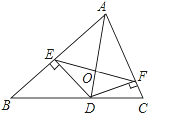
【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
【答案】(1)详见解析;(2) 垂直,理由详见解析;(3)四边形AEDF的面积为4﹣![]() .
.
【解析】
(1)由角平分线的性质直接可得到DE=DF;
(2)可证明△AED≌△AFD,可知AE=AF,利用线段垂直平分线的判定可证明AD是EF的垂直平分线,可证得结论;
(3)设△CDF的面积为x,则可分别表示出△BED、△ADE的面积,利用三角形的面积可分别表示出DE和DF,根据DE=DF可得到关于x的方程,可求得x的值,进一步可求得四边形AEDF的面积.
(1)∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,∴DE=DF(角平分线的性质);
(2)垂直.理由如下:
∵AD是△ABC的角平分线,∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,∵
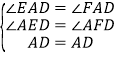 ,∴Rt△AED≌Rt△AFD(AAS),∴AE=AF,∴点A在线段EF的垂直平分线上,同理点D也在线段EF的垂直平分线上,∴AD⊥EF;
,∴Rt△AED≌Rt△AFD(AAS),∴AE=AF,∴点A在线段EF的垂直平分线上,同理点D也在线段EF的垂直平分线上,∴AD⊥EF;
(3)设S△CDF=x,则S△BDE=2x.
∵S△ACD=1,且△AED≌△AFD,∴S△AED=S△AFD=1﹣x,∴S△ABD=S△BDE+S△AED=2x+1﹣x=x+1,又S△ABD![]() ABDE,S△ACD
ABDE,S△ACD![]() ACDF,且AB=c,AC=b,∴
ACDF,且AB=c,AC=b,∴![]() cDE=x+1,
cDE=x+1,![]() bDF=1,∴DE
bDF=1,∴DE![]() ,DF
,DF![]() ,又由(1)可知DE=DF,∴
,又由(1)可知DE=DF,∴![]() ,解得:x
,解得:x![]() 1.
1.
∵△AED≌△AFD,∴S△AED=S△AFD=S△ACD﹣S△CDF=1﹣x,∴S四边形AEDF=2S△AED=2(1﹣x)=2[1﹣(![]() 1)]=4
1)]=4![]() ,即四边形AEDF的面积为4
,即四边形AEDF的面积为4![]() .
.

【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n | 2 | 3 | 4 | 5 | … |
a | 22﹣1 | 32﹣1 | 42﹣1 | 52﹣1 | … |
b | 4 | 6 | 8 | 10 | … |
c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系