题目内容
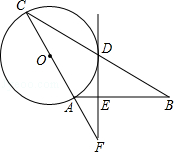
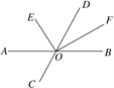
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
【答案】(1)∠EOF=90°;(2) ∠AOC的度数变化时,∠EOF的度数不变化,理由见解析.
【解析】
(1)根据对顶角、邻补角,可得∠BOD、∠AOD,根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案.
(1)由对顶角相等,得∠BOD=∠AOC=50°,
由OF平分∠BOD,得∠DOF=![]() ∠BOD=
∠BOD=![]() ×50°=25°,
×50°=25°,
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=![]() ∠AOD=
∠AOD=![]() ×130°=65°,
×130°=65°,
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数不变化,
由OF平分∠BOD,得∠DOF=![]() ∠BOD,
∠BOD,
由OE平分∠AOD,得∠DOE=![]() ∠AOD,
∠AOD,
由角的和差,得∠EOF=∠DOF+∠DOE=![]() ∠BOD+
∠BOD+![]() ∠AOD=
∠AOD=![]() (∠AOD+∠BOD)=
(∠AOD+∠BOD)=![]() ∠AOB=90°.
∠AOB=90°.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |
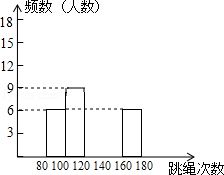
请结合图表解答下列问题:
(1)表中的m=;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.