题目内容
【题目】如图,二次函数Y=﹣ ![]() x2﹣
x2﹣ ![]() x+2象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是 .
x+2象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是 . 
【答案】8
【解析】解:在y=﹣ ![]() x2﹣
x2﹣ ![]() x+2中,当x=0时,y=2, ∴C(0,2),
x+2中,当x=0时,y=2, ∴C(0,2),
当y=0时,有﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,解得:x=﹣4或x=1,
x+2=0,解得:x=﹣4或x=1,
∴点A(﹣4,0)、B(1,0),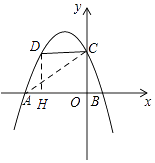
∵点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m,﹣ ![]() m2﹣
m2﹣ ![]() m+2),
m+2),
过点D作DH⊥x轴于点H,则DH=﹣ ![]() m2﹣
m2﹣ ![]() m+2,AH=m+4,HO=﹣m,
m+2,AH=m+4,HO=﹣m,
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,
∴S= ![]() (m+4)×(﹣
(m+4)×(﹣ ![]() m2﹣
m2﹣ ![]() m+2)+
m+2)+ ![]() (﹣
(﹣ ![]() m2﹣
m2﹣ ![]() m+2+2)×(﹣m),
m+2+2)×(﹣m),
=﹣m2﹣4m+4
=﹣(m+2)2+8,(﹣4<m<0);
则m=﹣2时,S取得最大值,最大值为8,
所以答案是:8.
【考点精析】本题主要考查了二次函数的最值和抛物线与坐标轴的交点的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

练习册系列答案
相关题目