题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.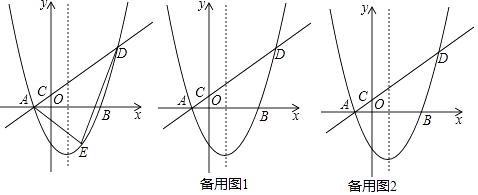
(1)直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为 ![]() 时,求抛物线的函数表达式;
时,求抛物线的函数表达式;
(3)设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.
【答案】
(1)
解:令y=0,则ax2﹣2ax﹣3a=0,
解得x1=﹣1,x2=3
∵点A在点B的左侧,
∴A(﹣1,0),
如图1,作DF⊥x轴于F,
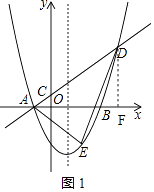
∴DF∥OC,
∴ ![]() =
= ![]() ,
,
∵CD=4AC,
∴ ![]() =
= ![]() =4,
=4,
∵OA=1,
∴OF=4,
∴D点的横坐标为4,
代入y=ax2﹣2ax﹣3a得,y=5a,
∴D(4,5a),
把A、D坐标代入y=kx+b得 ![]() ,
,
解得 ![]() ,
,
∴直线l的函数表达式为y=ax+a
(2)
解:如图2,过点E作EH∥y轴,交直线l于点H,
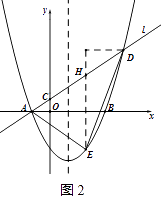
设E(x,ax2﹣2ax﹣3a),则H(x,ax+a).
∴HE=(ax+a)﹣(ax2﹣2ax﹣3a)=﹣ax2+3ax+4a,
由 ![]() 得x=﹣1或x=4,
得x=﹣1或x=4,
即点D的横坐标为4,
∴S△ADE=S△AEH+S△DEH= ![]() (﹣ax2+3ax+4a)=﹣
(﹣ax2+3ax+4a)=﹣ ![]() a(x﹣
a(x﹣ ![]() )2+
)2+ ![]() a.
a.
∴△ADE的面积的最大值为 ![]() a,
a,
∴ ![]() a=
a= ![]() ,
,
解得:a= ![]() .
.
∴抛物线的函数表达式为y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]()
(3)
解:已知A(﹣1,0),D(4,5a).
∵y=ax2﹣2ax﹣3a,
∴抛物线的对称轴为x=1,
设P(1,m),
①若AD为矩形的边,则AD∥PQ,且AD=PQ,
则Q(﹣4,21a),
m=21a+5a=26a,则P(1,26a),
∵四边形ADPQ为矩形,
∴∠ADP=90°,
∴AD2+PD2=AP2,
∴52+(5a)2+(1﹣4)2+(26a﹣5a)2=(﹣1﹣1)2+(26a)2,
即a2= ![]() ,
,
∵a>0,
∴a= ![]() ,
,
∴P1(1, ![]() ),
),
②若AD是矩形的一条对角线,则AD与PQ互相平分且相等.
∴xD+xP=xA+xQ,yD+yA=yP+yQ,
∴xQ=2,
∴Q(2,﹣3a).
∴yP=8a
∴P(1,8a).
∵四边形APDQ为矩形,
∴∠APD=90°
∴AP2+PD2=AD2
∴(﹣1﹣1)2+(8a)2+(1﹣4)2+(8a﹣5a)2=52+(5a)2
即a2= ![]() ,
,
∵a>0,
∴a= ![]()
∴P2(1,4)
综上所述,以点A、D、P、Q为顶点的四边形能成为矩形,点P的坐标为(1, ![]() )或(1,4)
)或(1,4)
【解析】(1)由抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于两点A、B,求得A点的坐标,作DF⊥x轴于F,根据平行线分线段成比例定理求得D的坐标,然后利用待定系数法法即可求得直线l的函数表达式.(2)设点E(m,ax2﹣2ax﹣3a),知HE=(ax+a)﹣(ax2﹣2ax﹣3a)=﹣ax2+3ax+4a,根据直线和抛物线解析式求得点D的横坐标,由S△ADE=S△AEH+S△DEH列出函数解析式,根据最值确定a的值即可;(3)分以AD为矩形的对角线和以AD为矩形的边两种情况利用矩形的性质确定点P的坐标即可.

【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n | 2 | 3 | 4 | 5 | … |
a | 22﹣1 | 32﹣1 | 42﹣1 | 52﹣1 | … |
b | 4 | 6 | 8 | 10 | … |
c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系