��Ŀ����
����Ŀ���Ȱ�ѧϰ��С��ͬѧ��������������������ֲ��ϣ�
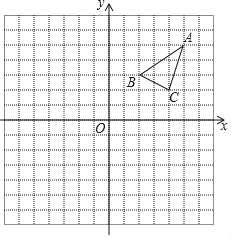
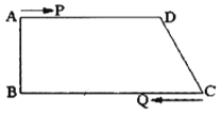
��x���������������ǵ�����ֱ�Ϊ��a��0���ͣ�c��0�����������������ɵ��߶εij�Ϊ|a��c|��ͬ��������y���ϵ���������ֱ�Ϊ��0��b���ͣ�0��d�����������������ɵ��߶εij�Ϊ|b��d|����ͼ1����ֱ������ϵ�е���������P1��P2��������ֱ�Ϊ��a��b���ͣ�c��d�����ֱ���������������������ƽ���ߣ�����һ��ֱ�������Σ�����ֱ�DZ�P1Q=|a��c|��P2Q=|b��d|�����ù��ɶ����ɵã��߶�P1P2�ij�Ϊ![]() ��
��
����������ϣ��ش���������⣺
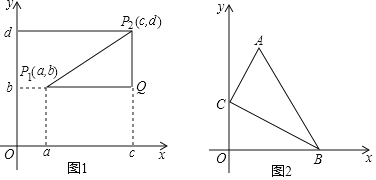
��1����ƽ��ֱ������ϵ�У���֪A��6����1����B��6��5�������߶�AB�ij�Ϊ ��
��2������C��y���ϣ���D�������ǣ���3��0������CD=6�����C�������� ��
��3����ͼ2����ֱ������ϵ�У���A��B������ֱ�Ϊ��1��4���ͣ�3��0������C��y���ϵ�һ�����㣬��A��B��C���㲻��ͬһ��ֱ���ϣ����ABC�ܳ�����Сֵ��
���𰸡���1��6����2��![]() ��
��![]() ����3��
����3��![]() ��
��
��������
��1�������߶γ��ȼ��㷽�����㼴�ɣ�
��2����C������Ϊ��0��b���������߶γ��ȼ��㷽�����㼴�ɣ�
��3���ҵ���A����y��ĶԳƵ�A'����1��4��������A'B��y���ڵ�C����ʱ��ABC�ܳ�����С��Ȼ������߶γ��ȼ��㷽��������⣮
�⣺��1����A��6����1����B��6��5����
��![]() ��
��
�ʴ�Ϊ��6��
��2����C��������0��b����
����Rt��OCD��CD2=OC2+OD2��������3��0��2+��0��b��2=62��
���![]() ��
��
����C������Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3����ͼ����A�����y��ĶԳƵ�ΪA'�����A'������Ϊ����1��4����A'C = AC��
�ߡ�ABC���ܳ�=AB+ AC+CB=AB+ A'C+CB�������߶�AB�ij�Ϊ��ֵ��
�൱C��ΪA'B��y��Ľ���ʱ����ʱA'B��ΪA'C+CB����Сֵ����ABC���ܳ���С��
��ʱ��ABC���ܳ�=AB+A'C+CB= AB+A'B��
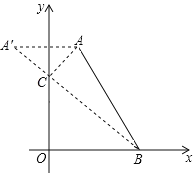
�ߵ�A��B������ֱ�Ϊ��1��4���ͣ�3��0����
��AB![]() 2
2![]() ��
��![]() ��
��
���ԡ�ABC���ܳ�����СֵΪ![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�