题目内容
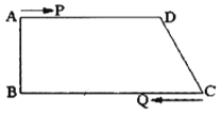
【题目】如图，在四边形ABCD中，AD//BC，
，AD=24 cm，AB=8 cm, BC=26 cm，动点P从A开始沿AD边向D以1cm/s的速度运动；Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发，当其中一点到达端点时，另外一点也随之停止运动.
（1）当运动时间为t秒时，用含t的代数式表示以下线段的长： AP=________, BQ=__________；
（2）当运动时间为多少秒时，四边形PQCD为平行四边形？
（3）当运动时间为多少秒时，四边形ABQP为矩形？
【答案】（1）t，26-3t；（2）运动时间为6秒时，四边形PQCD为平行四边形．（3）运动时间为
秒时，四边形ABQP为矩形．
【解析】
（1）根据题意可直接得出；
（2）由在梯形ABCD中，AD∥BC，可得当PD=CQ时，四边形PQCD是平行四边形，即可得方程：24-t=3t，解此方程即可求得答案；
（3）由在梯形ABCD中，AD∥BC，∠B=90°，可得当AP=BQ时，四边形ABQP是矩形，即可得方程：t=26-3t，解此方程即可求得答案．
解：（1）由题意知AP=t，BQ=26-3t，
故答案为：t，26-3t；
（2）由题意可得：PD=AD-AP=24-t，QC=3t，
∵AD∥BC，
∴PD∥QC，
设当运动时间为t秒时PD=QC，此时四边形PQCD为平行四边形．
由PD=QC得，24-t=3t，
解得：t=6，
∴当运动时间为6秒时，四边形PQCD为平行四边形．
（3）∵AD∥BC，
∴AP∥BQ，
设当运动时间为t秒时AP=BQ，四边形ABQP为平行四边形．
由AP=BQ得：t=26-3t，
解得：t=，
又∵∠B=90°
∴平行四边形ABQP为矩形．
∴当运动时间为秒时，四边形ABQP为矩形．
