题目内容
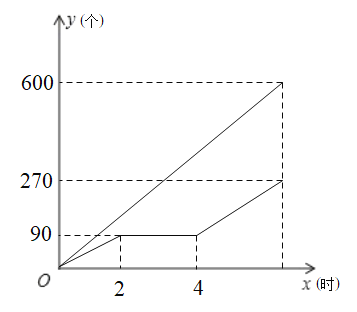
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完成这批零件,甲车间工作了8个小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止.设甲、乙两车间各自加工零件的数量为![]() (个),甲车间加工的时间为
(个),甲车间加工的时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲车间每小时加工零件的个数为_________个;这批零件的总个数为__________个;
(2)求乙车间维护设备后,乙车间加工零件的数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在加工这批零件的过程中,当甲、乙两车间共同加工完成810个零件时,求甲车间加工的时间.
【答案】(1)75,870;(2)![]() ;(3)甲车间加工的时间为7.5个小时.
;(3)甲车间加工的时间为7.5个小时.
【解析】
(1)根据图像可知甲8个小时加工了600个零件,乙8个小时加工了270个零件,据此填空即可;
(2)设![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,由图像知该函数过点
,由图像知该函数过点![]() ,利用待定系数法求解即可;
,利用待定系数法求解即可;
(3)设甲车间加工了x个小时,根据甲乙总共加工810个零件列方程求解即可.
解:(1)由图像得甲8个小时加工了600个零件,![]() (个),
(个),
![]() (个),
(个),
所以甲车间每小时加工零件的个数为75个;这批零件的总个数为870个;
(2)设![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,由图像知该函数过点
,由图像知该函数过点![]() ,
,
将点![]() 代入得
代入得![]()
解得![]()
所以![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ;
;
(3)由图像得乙的设备维修了2个小时,乙每小时加工![]() 个
个
设甲车间加工了x个小时,则乙车间加工了![]() 个小时
个小时
根据题意得![]()
解得![]()
所以甲车间加工的时间为7.5个小时.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
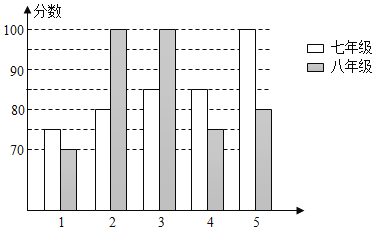
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.