题目内容
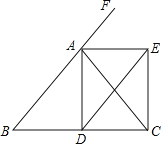
【题目】如图,![]() ,
,![]() 是
是![]() 边的中点,
边的中点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
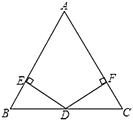
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的周长.
的周长.
【答案】(1)详见解析;(2)12.
【解析】
(1)先利用等腰三角形等边对等角得出∠B=∠C,再利用AAS证明△BDE≌△CDF,即可得出结论;
(2)先证明△ABC是等边三角形,然后根据含30°的直角三角形的性质求出等边三角形的边长,则周长可求.
(1)证明:∵AB=AC
∴∠B=∠C,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,
∵D是BC边的中点,
∴BD=CD,
在△BDE和△CDF中, ,
,
∴△BDE≌△CDF(AAS)
∴BE=CF;
(2)解:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠BED=∠CFD=90°,
∴∠BDE=∠CDF=30°,
∴BD=2BE=2=CD,
∴BC=4,
∴△ABC周长=4×3=12.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
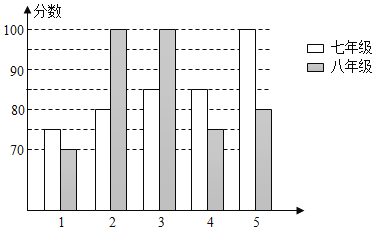
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.