题目内容
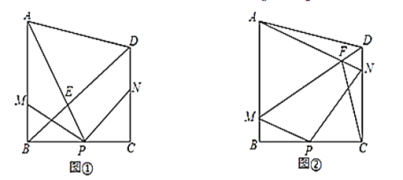
【题目】如图，在△ABC中，BD、CE分别是∠ABC和∠ACB的平分线，AM⊥CE于P，交BC于M，AN⊥BD于Q，交BC于N，∠BAC=110°，AB=6，AC=5，MN=2，结论①AP=MP；②BC=9；③∠MAN=35°；④AM=AN.其中不正确的有（ ）
A.4个B.3个C.2个D.1个
【答案】D
【解析】
利用三角形的角平分线的性质得出角相等，通过证明三角形全等得出边相等即可判断①②的对错，利用三角形内角和等于180°、三角形外角和以及等角替换证明③④的对错即可.
解：
CE是∠ACB的平分线且AM⊥CE
∴CM=AC
在MCP和APC中
∴MCPAPC
同理可证ABQBNQ
∴AM=AP（故①正确），BN=AB
∴BC=BN+CN-MN=AB+AC-MN=6+5-2=9（故②正确）
根据题意有
=
=75°
∴
,故③正确
根据上述可知
∴AM≠AN，故④错误
故选D.
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】某驻村扶贫小组为解决当地贫困问题，带领大家致富．经过调查研究，他们决定利用当地生产的甲乙两种原料开发A，B两种商品，为科学决策，他们试生产A、B两种商品100千克进行深入研究，已知现有甲种原料293千克，乙种原料314千克，生产1千克A商品，1千克B商品所需要的甲、乙两种原料及生产成本如下表所示．
甲种原料（单位：千克） | 乙种原料（单位：千克） | 生产成本（单位：元） | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克，生产A、B两种商品共100千克的总成本为y元，根据上述信息，解答下列问题：
（1）求y与x的函数解析式（也称关系式），并直接写出x的取值范围；
（2）x取何值时，总成本y最小？
