题目内容
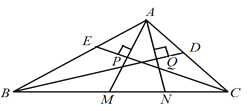
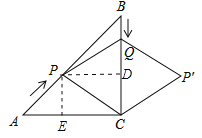
【题目】如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P 从点A 出发，沿AB方向以每秒
cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm 的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′.设Q点运动的时间 t 秒，若四边形QPCP′为菱形，则 t 的值为（ ）
A. B. 2 C. 2 D. 4
【答案】B
【解析】
作PD⊥BC于D，PE⊥AC于E，AP=
t，BQ=t，（0≤t＜6），由△ABC为直角三角形得∠A=∠B=45°，则可判断△APE为等腰直角三角形，所以PE=AE=
AP=t，由四边形PECD为矩形得到DC=PE=tcm，然后根据菱形的性质得到PQ=PC，根据等腰三角形的性质得到QD=DC= tcm，由BC=6，解方程得到满足条件的t的值．
作PD⊥BC于D，PE⊥AC于E，如图，AP=t，BQ=tcm，（0≤t＜6）
∵∠C=90°，AC=BC=6cm，∴△ABC为直角三角形，∴∠A=∠B=45°，∴△APE为等腰直角三角形，∴PE=AE=AP=tcm，
∵四边形PECD为矩形，∴DC=PE=tcm．
∵四边形QPCP′为菱形，∴PQ=PC．∵PD⊥BC，∴QD=DC= tcm．∵BC=BQ+QD+DC=6，∴t+t+t=6，解得：t=2．
故选B．
【题目】2019 年 3 月 31 日，南京地铁新的价格方案正式实施，实行消费累进优惠．普通成人每月持卡乘坐地铁，当消费累计金额不超过 150 元时，每次乘坐地铁的票价打 9．5 折；当消费累计金 额超过 150 元时，达到规定的消费累计金额后的乘次，票价所打折扣如下表所示：
消费累计金额 | 折扣 |
| 9折 |
| 8折 |
| 9.5折 |
小明上、下班每次乘坐的地铁单程票价为 10元，2019年 4月份他上、下班持卡共乘坐了 40次．
（1）填表：
第1 次 | 第2 次 | … | 第15次 | 第16次 | 第17次 | … | |
消费累计 金额（元） | 9.5 | 19 | … | 142.5 | 152 | … |
span>
（2）小明当月第几次乘车后，消费累计金额超过 20元？（用一元一次不等式解决问题）
（3）小明 4月份上、下班持卡乘坐地铁的消费累计金额为 元．
