题目内容
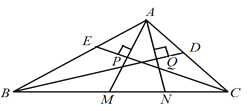
【题目】如图,在四边形![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.点
匀速移动.点![]() 同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为
同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为![]() .
.
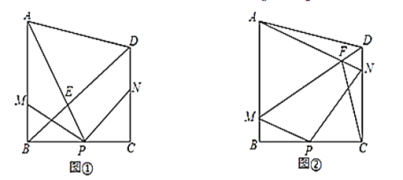
(1)如图①,
①当![]() 为何值时,点
为何值时,点![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?并求出相应的
全等?并求出相应的![]() 的值;
的值;
②连接![]() 交于点
交于点![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
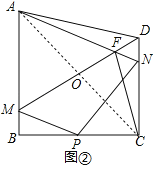
(2)如图②,连接![]() 交于点
交于点![]() .当
.当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)①![]() ,
,![]() 或
或![]() ,
,![]() ;②
;②![]() ;(2)见解析
;(2)见解析
【解析】
(1)①当![]() 时或当
时或当![]() 时,分别列出方程即可解决问题;
时,分别列出方程即可解决问题;
②当![]() 时,由
时,由![]() ,推出
,推出![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
(2)如图②中,连接![]() 交
交![]() 于
于![]() 只要证明
只要证明![]() ,推出
,推出![]() ,可得
,可得![]() ,
,![]() ,推出
,推出![]() ,即
,即![]() ;
;
解:(1)①![]() ,
,
![]() 当
当![]() 时,有
时,有![]() ,即
,即![]() ①
①
![]() ②
②
由①②可得![]() ,
,![]() .
.
当![]() 时,有
时,有![]() ,
,![]() ,即
,即![]() ③
③
![]() ④,
④,
由③④可得![]() ,
,![]() .
.
综上所述,当![]() ,
,![]() 或
或![]() ,
,![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等;
全等;
②![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
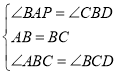 ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ;
;
(2)![]() 当
当![]() ,
,![]() 时,
时,![]() ,而
,而![]() ,
,
![]() ,
,
![]() 点
点![]() 在点
在点![]() 、
、![]() 之间,
之间,
![]() ,
,![]() ,
,
![]() ,
,
如图②中,连接![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
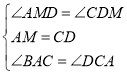 ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?