题目内容
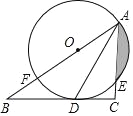
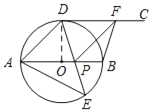
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE= 时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE= 时,四边形BFDP是正方形.
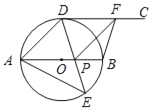
【答案】(1)详见解析;(2)①67.5°;②90°.
【解析】
(1)连接OD,由切线的性质得到∠ODF=90°,再由已知得到∠AOD=2∠AED=90°,从而得到∠ODF=∠AOD,进而证明CD∥AB;
(2)①根据菱形的性质进行角度运算即可得出;
②根据正方形的性质运算角度即可得出.
解:(1)如图,连接OD,
∵射线DC切⊙O于点D,
∴OD⊥CD,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,即∠ODF=∠AOD,
∴CD∥AB.

(2)①连接AF与DP交于点G,如图所示,
∵四边形ADFP是菱形,∠AED=45°,OA=OD,
∴AF⊥DP,∠AOD=90°,∠DAG=∠PAG,
∴∠AGE=90°,∠DAO=45°,
∴∠EAG=45°,∠DAG=∠PAG=22.5°,
∴∠EAD=∠DAG+∠EAG=22.5°+45°=67.5°,
故答案为:67.5°;
②∵四边形BFDP是正方形,
∴BF=FD=DP=PB,
∠DPB=∠PBF=∠BFD=∠FDP=90°,
∴此时点P与点O重合,
∴此时DE是直径,
∴∠EAD=90°,
故答案为:90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目