题目内容
【题目】已知O为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() .与
.与![]() 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,![]() ,
,![]() ,点A,C在直线
,点A,C在直线![]() 上.
上.
(1)求点C的坐标;
(2)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(3)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线![]() 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求![]() 的最小值.
的最小值.
【答案】(0,3)或(0,-3);若c=3,当y随x的增大而增大时,x≤-1;若c=-3,当y随x的增大而增大时,x≥1;![]()
【解析】
试题(1)令x=0,求出点C的坐标,根据OC的距离为3得出点C的坐标;(2)根据![]() <0得出
<0得出![]() ,
,![]() 异号,①、当C(0,3),把C(0,3)代入
异号,①、当C(0,3),把C(0,3)代入![]() =-3x+t得出t的值,将A(
=-3x+t得出t的值,将A(![]() ,0)代入
,0)代入![]() =-3x+3得出
=-3x+3得出![]() 的值,根据
的值,根据![]() ,
,![]() 异号以及
异号以及![]() =4得出
=4得出![]() 的值,然后将其代入二次函数解析式求出解析式,然后根据顶点式求出y随x增大而增大的x的取值范围;②当C(0,-3)时,用同样的方法进计算;(3)若c=3,则
的值,然后将其代入二次函数解析式求出解析式,然后根据顶点式求出y随x增大而增大的x的取值范围;②当C(0,-3)时,用同样的方法进计算;(3)若c=3,则![]() =-
=-![]() -2x+3=-
-2x+3=-![]() +4,
+4,![]() =-3x+3,
=-3x+3,![]() 向左平移n个单位后则解析式为:
向左平移n个单位后则解析式为:![]() +4,则当x≤-1-n时,y随x的增大而增大,
+4,则当x≤-1-n时,y随x的增大而增大,![]() 向下平移n个单位后则解析式为:
向下平移n个单位后则解析式为:![]() =-3x+3-n,要使平移后直线与P有公共点,则当x=-1-n,
=-3x+3-n,要使平移后直线与P有公共点,则当x=-1-n,![]() ≥
≥![]() ,然后求出n的取值范围;若c=-3,利用同样的方法进行计算,然后将所求的二次函数化成顶点式,求出最小值.
,然后求出n的取值范围;若c=-3,利用同样的方法进行计算,然后将所求的二次函数化成顶点式,求出最小值.
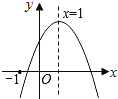
试题解析:(1)令x=0 则y=c ∴C(0,c) ∵OC的距离为3 ∴![]() =3 即c=±3
=3 即c=±3
∴C(0,3)或(0,-3)
(2)∵![]() <0 ∴
<0 ∴![]() ,
,![]() 异号
异号
①若C(0,3) 即c=3 把C(0,3)代入![]() =-3x+t,则0+t=3 即t=3 ∴
=-3x+t,则0+t=3 即t=3 ∴![]() =-3x+3
=-3x+3
把A(![]() ,0)代入
,0)代入![]() =-3x+3,则-3
=-3x+3,则-3![]() +3=0 解得:
+3=0 解得:![]() =1
=1
∴A(1,0) ∵![]() ,
,![]() 异号
异号![]() =1>0 ∴
=1>0 ∴![]() <0
<0
∵![]() =4 ∴
=4 ∴![]() =-3 则B(-3,0) 代入
=-3 则B(-3,0) 代入![]() =
=![]() +bx+3得:a=-1,b=-2
+bx+3得:a=-1,b=-2
∴![]() =-
=-![]() -2x+3=-
-2x+3=-![]() +4,则当x≤-1时,y随x的增大而增大.
+4,则当x≤-1时,y随x的增大而增大.
②若C(0,-3) 即c=-3 把C(0,-3)代入![]() =-3x+t,则0+t=-3 即t=-3 ∴
=-3x+t,则0+t=-3 即t=-3 ∴![]() =-3x-3
=-3x-3
把A(![]() ,0)代入
,0)代入![]() =-3x-3,则-3
=-3x-3,则-3![]() -3=0 解得:
-3=0 解得:![]() =-1
=-1
∴A(-1,0) ∵![]() ,
,![]() 异号
异号![]() =-1<0 ∴
=-1<0 ∴![]() >0
>0
∵![]() =4 ∴
=4 ∴![]() =3 则B(3,0) 代入
=3 则B(3,0) 代入![]() =
=![]() +bx+3得:a=1,b=-2
+bx+3得:a=1,b=-2
∴![]() =
=![]() -2x-3=
-2x-3=![]() -4,则当x≥1时,y随x的增大而增大.
-4,则当x≥1时,y随x的增大而增大.
综上所述:若c=3,当y随x的增大而增大时,x≤-1;若c=-3,当y随x的增大而增大时,x≥1.
(2)①若c=3,则![]() =-
=-![]() -2x+3=-
-2x+3=-![]() +4,
+4,![]() =-3x+3
=-3x+3
![]() 向左平移n个单位后则解析式为:
向左平移n个单位后则解析式为:![]() +4 则当x≤-1-n时,y随x的增大而增大.
+4 则当x≤-1-n时,y随x的增大而增大.
![]() 向下平移n个单位后则解析式为:
向下平移n个单位后则解析式为:![]() =-3x+3-n
=-3x+3-n
要使平移后直线与P有公共点,则当x=-1-n,![]() ≥
≥![]()
即![]() ≥-3(-1-n)+3-n 解得:n≤-1
≥-3(-1-n)+3-n 解得:n≤-1
∵n>0 ∴n≤-1不符合条件,应舍去.
②若c=-3,则![]() =
=![]() -2x-3=
-2x-3=![]() -4,
-4,![]() =-3x-3
=-3x-3
![]() 向左平移n个单位后则解析式为:
向左平移n个单位后则解析式为:![]() -4 则当x≥1-n时,y随x的增大而增大.
-4 则当x≥1-n时,y随x的增大而增大.
![]() 向下平移n个单位后则解析式为:
向下平移n个单位后则解析式为:![]() =-3x-3-n
=-3x-3-n
要使平移后直线与P有公共点,则当x=1-n,![]() ≥
≥![]()
即-3(1-n)-3-n≥![]() -4 解得:n≥1
-4 解得:n≥1
综上所述,n≥1.
2![]() -5n=2
-5n=2![]() ∴当n=
∴当n=![]() 时,2
时,2![]() -5n的小值为-
-5n的小值为-![]()