题目内容
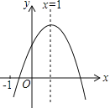
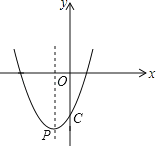
【题目】已知抛物线y=-x2+4交x轴于A,B两点,顶点是C.
(1)求△ABC的面积;
(2)若点P在抛物线y=-x2+4上, 且S△PAB=![]() S△ABC,求点P的坐标。
S△ABC,求点P的坐标。
【答案】(1)8;(2)点P的坐标为:(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2).
,-2).
【解析】
(1)根据抛物线的性质得到A(-2,0),B(2,0),C(0,4),所以△ABC是底边为4,高为4的等腰三角形,利用三角形的面积公式可以求出三角形的面积.
(2)根据△PAB的面积是△ABC的面积的一半,得到点P的纵坐标为±2,然后代入抛物线可以求出点P的横坐标,确定点P的坐标.
(1)A(-2,0),B(2,0),C(0,4).
∴S△ABC=![]() ×4×4=8.
×4×4=8.
所以△ABC的面积是8.
(2)∵S△PAB=![]() S△ABC
S△ABC
∴点P的纵坐标为±2,
当y=2时,代入抛物线有:2=-x2+4,得:x=±![]() .
.
当y=-2时,代入抛物线有:-2=-x2+4,得:x=±![]() .
.
所以点P的坐标为:(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2).
,-2).

练习册系列答案
相关题目
【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前40天每天的价格y(元/件)与时间t(天)的函数关系式为:y=![]() t+25(1≤t≤40且t为整数);
t+25(1≤t≤40且t为整数);
(1)认真分析表中的数据,用所学过的知识确定m(件)与t(天)之间是满足一次函数的关系还是二次函数的关系?并利用这些数据求m(件)与t(天)之间得函数关系式;
(2)请计算40天中哪一天的日销售利润最大,最大日销售利润是多少?