题目内容
【题目】如图 1,在第四象限的矩形 ABCD,点 A 与坐标原点 O 重合,且 AB=4,AD=3.点 Q 从 B点出发以每秒 1 个单位长度的速度沿 B→C→D 运动,当点 Q 到达点 D 时,点 Q 停止运动,设点 Q 运动的时间为 t 秒.
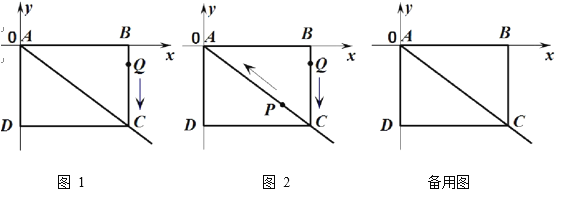
⑴请直接写出图 1 中,点 C 的坐标,并求出直线 OC 的表达式;
⑵求△ACQ 的面积 S 关于 t 的函数关系式,并写出 t 的取值范围;
⑶如图 2,当点 Q 开始运动时,点 P 从 C 点出发以每秒 2 个单位长度的速度运动向点 A运动,当点 P 到达 A 点时点 Q 和点 P 同时停止运动,当△QCP 与△ABC 相似时,求出相应的 t 值.
【答案】(1)(4,-3);![]() (2)
(2)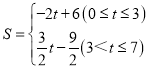 (3)
(3)![]() 或
或![]()
【解析】
(1)根据四边形是矩形及AB=4,AD=3可直接写成点 C 的坐标,并用待定系数法求出直线 OC 的表达式;
(2)分点Q在线段BC上及线段CD上两种情况讨论;
(3)先确定Q点的位置,再分![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(1)根据题意得:
点 C 的坐标为(4,-3)
设直线 OC 的表达式为:y=kx
则-3=4k k=-![]()
∴直线 OC 的表达式为:![]()
(2)当点Q在线段BC上,即0≤t≤3时,
S=![]()
当点Q在线段CD上,即3<t≤7时,
![]()
∴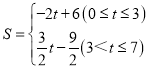
(3)∵四边形ABCD是矩形,AB=4,AD=3.
∴AC=5
∴P点从C点到A点需要2.5秒,则Q点在BC上运动
当△QCP∽ACB时,![]() ,
,
则![]() ,解得:
,解得:![]()
当△QCP∽BCA时,![]() ,
,
则![]() ,解得:
,解得:![]()
故当△QCP 与△ABC 相似时,![]() 或
或![]()

练习册系列答案
相关题目