题目内容
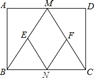
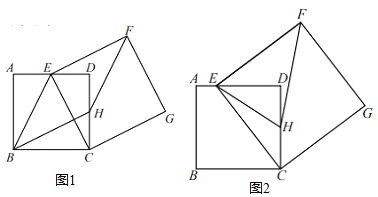
【题目】如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
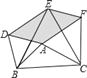
【答案】(1)四边形ADEF是平行四边形;
(2)∠BAC=150°时,四边形ADEF是矩形;
(3)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.
【解析】
(1)四边形ADEF平行四边形.根据△ABD,△EBC都是等边三DAE角形容易得到全等条件证明△DBE≌△ABC,然后利用全等三角形的性质和平行四边形的判定可以证明四边形ADEF平行四边形;
(2)若边形ADEF是矩形,则∠FAD=90°,然后根据已知可以得到∠BAC=150°;
(3)当∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
(1)四边形ADEF是平行四边形.理由如下:
∵△ABD,△EBC都是等边三角形,∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°,∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.
在△DBE和△ABC中,∵BD=BA,∠DBE=∠ABC,BE=BC,∴△DBE≌△ABC,∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可证:AD=EF,∴四边形ADEF平行四边形.
(2)当∠BAC=150°时,四边形ADEF是矩形.理由如下:
∵四边形ADEF是矩形,∴∠FAD=90°,∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°,∴∠BAC=150°时,四边形ADEF是矩形.
(3)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.理由如下:
若∠BAC=60°,则∠DAF=360°﹣∠BAC﹣∠DAB﹣∠FAC=360°﹣60°﹣60°﹣60°=180°.
此时,点A、D、E、F四点共线,∴以A、D、E、F为顶点的四边形不存在.

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.