题目内容
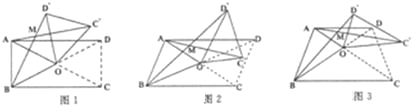
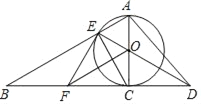
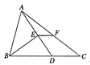
【题目】如图,在![]() 中,,点
中,,点![]() 在
在![]() 上,且
上,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连结
的中点,连结![]() .若四边形DCFE和△BDE的面积都为3,则△ABC的面积为____.
.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为____.
【答案】10
【解析】
首先利用等腰三角形的性质得到点E是AD的中点,可得EF是△ACD的中位线,则EF∥CD,EF=![]() CD,进而可证明△AEF∽△ADC,然后利用相似三角形面积的比等于相似比的平方求得△ADC的面积,由点E是AD的中点得△BDE和△BAE面积相等,利用
CD,进而可证明△AEF∽△ADC,然后利用相似三角形面积的比等于相似比的平方求得△ADC的面积,由点E是AD的中点得△BDE和△BAE面积相等,利用![]()
![]() 即可求解.
即可求解.
解:∵BE平分∠ABC,BD=BA,
∴BE是△ABD的中线,
∴点E是AD的中点,
又∵F是AC的中点,
∴EF是△ADC的中位线,
∴EF∥CD,EF=![]() CD,
CD,
∴△AEF∽△ADC,
∴S△AEF:S△ADC=1:4,
∴S△AEF:S四边形DCFE=1:3,
∵四边形DCFE的面积为3,
∴S△AEF=1,
∴S△ADC =S△AEF+ S四边形DCFE =1+3=4,
∵点E是AD的中点,△BDE的面积为3,
∴ ![]() =3,
=3,
∴![]() =3+3+4=10.
=3+3+4=10.
故答案为:10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目