��Ŀ����
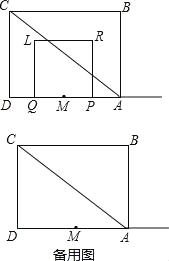
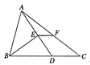
����Ŀ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������ǡ�DOC=��������DOC����ʱ�뷽����ת�õ���D��OC�䣨0�㣼��ת�ǣ�90�㣩����AC�䡢BD�䣬AC����BD���ཻ�ڵ�M��
��1�����ı���ABCD�Ǿ���ʱ����ͼ1�������AC����BD���������ϵ�Լ���AMB����Ĵ�С��ϵ����֤����IJ��룻
��2�����ı���ABCD��ƽ���ı���ʱ����ͼ2����֪AC=BD��������ʱAC����BD���������ϵ�Լ���AMB����Ĵ�С��ϵ����֤����IJ��룻
��3�����ı���ABCD�ǵ�������ʱ����ͼ3��AD��BC����ʱ��1��AC����BD���������ϵ�Ƿ��������AMB����Ĵ�С��ϵ�Ƿ����������֤����ֱ��д�����ۣ�
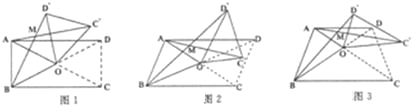
���𰸡�(1) AC��=BD�䣬��AMB=�������ɼ���������2��AC��=kBD�䣬��AMB=�������ɼ���������3��AC��=BD���������AMB=��������
��������
��1�����ݾ��ε����ʼ���֮��Ĺ�ϵ֤����BOD��ա�AOC�䣬�ó���Ӧ�߶�Ӧ����ȣ��������ɵó����ۣ�
��2���Ƚ��м��裬Ȼ�����ƽ���ı��ε����ʼ����������α�����ϵ���ɵó��𰸣�
��3����֤��BOD��ա�C��OA����AC��=BD�䣬��OBD��=��OC��A�١�OAC�䣬�Ӷ��ó���AMB�٦���
�⣺��1��AC��=BD�䣬��AMB=����
֤�����ھ���ABCD�У�AC=BD��OA=OC=![]() AC��OB=OD=
AC��OB=OD=![]() BD��
BD��
��OA=OC=OB=OD��
�֡�OD=OD�䣬OC=OC�䣬
��OB=OD��=OA=OC�䣬
�ߡ�D��OD=��C��OC��
��180��-��D��OD=180��-��C��OC��
���BOD��=��AOC�䣬
���BOD��ա�AOC�䣬
��BD��=AC�䣬
���OBD��=��OAC�䣬
��BD����OA�ཻ�ڵ�N��
���BNO=��ANM��
��180��-��OAC��-��ANM=180��-��OBD��-��BNO��
����AMB=��AOB=��COD=����
����������BD��=AC�䣬��AMB=����
��2��AC��=kBD�䣬��AMB=����
֤������ƽ���ı���ABCD�У�OB=OD��OA=OC��
�֡�OD=OD�䣬OC=OC�䣬
��OB��OA=OD�䣺C�䣬
�ߡ�D��OD=��C��OC��
��180��-��D��OD=180��-��C��OC��
���BOD��=��AOC�䣬
���BOD��ס�AOC�䣬
��BD�䣺AC��=OB��OA=BD��AC��
��AC=kBD��
��AC��=kBD�䣬
�ߡ�BOD��ס�AOC�䣬
��BD����OA�ཻ�ڵ�N��Z+X+X+K]
���BNO=��ANM��
��180��-��OAC��-��ANM=180��-��OBD��-��BNO������AMB=��AOB=����
����������AC��=kBD�䣬��AMB=����
��3��AC��=BD���������AMB=����������

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�����Ŀ��ijУҪ����ͬѧ����ͬѧ����ѡһ�˲μ���֪ʶ���������ѡ�β����������ijɼ����±���
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | |
��ͬѧ | 60 | 75 | 100 | 90 | 75 |
��ͬѧ | 70 | 90 | 100 | 80 | 80 |
�����ϱ�����������⣺
��1������±���
���� | ƽ���ɼ����֣� | ��λ�����֣� | �������֣� | ���� |
��ͬѧ | 80 | 75 | 75 | _____ |
��ͬѧ | �� �� | �� �� | �� �� | �� �� |
��2��������β����У��ɼ��Ƚ��ȶ���ͬѧ��˭����80�����ϣ���80�֣��ijɼ���Ϊ���㣬����ͬѧ����ͬѧ������β����е������ʸ��Ƕ��٣�
��3����������������ɼ��ﵽ80�����ϣ���80�֣��ͺܿ��ܻ��ɼ��ﵽ90�����ϣ���90�֣��ͺܿ��ܻ��һ�Ƚ�����ô����ΪӦѡ˭�μӱ����ȽϺ��ʣ�˵��������ɣ�