Question

【题目】如图，放置在水平桌面上的台灯灯臂AB长为42cm，灯罩BC长为32cm，底座厚度为2cm，灯臂与底座构成的∠BAD＝60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？

Answer 1

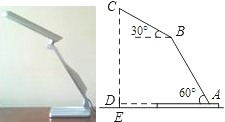
【答案】此时灯罩顶端C到桌面的高度CE是（2118）cm．

【解析】

过点B作BM⊥CE于点M，BF⊥DA于点F．在Rt△BCM和Rt△ABF中，通过解直角三角形可求出CM、BF的长，再由CE=CM+BF+ED即可求出CE的长．

过点B作BM⊥CE于点M，BF⊥DA于点F，如图所示．

在Rt△BCM中，∵BC=32cm，∠CBM=30°，∴CM=BCsin∠CBM=16cm．

在Rt△ABF中，AB=42cm，∠BAD=60°，∴BF=ABsin∠BAD=21cm．

∵∠ADC=∠BMD=∠BFD=90°，∴四边形BFDM为矩形，∴MD=BF，∴CE=CM+MD+DE=CM+BF+ED=16+212=2118（cm）．

答：此时灯罩顶端C到桌面的高度CE是（2118）cm．