题目内容
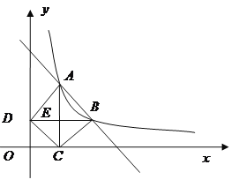
【题目】如图,在平面直角坐标系中,函数![]() (
(![]() ,是常数)的图像经过A(2,6),B(m,n),其中m>2.过点A作
,是常数)的图像经过A(2,6),B(m,n),其中m>2.过点A作![]() 轴垂线,垂足为C,过点
轴垂线,垂足为C,过点![]() 作轴垂线,垂足为
作轴垂线,垂足为![]() ,AC与BD交于点E,连结AD,
,AC与BD交于点E,连结AD,![]() ,CB.
,CB.
(1)若![]() 的面积为3,求m的值和直线
的面积为3,求m的值和直线![]() 的解析式;
的解析式;
(2)求证:![]() ;
;
(3)若AD//BC ,求点B的坐标 .
【答案】(1)![]() ,y=-2x+10;(2) 见解析;(3) B(4,3)
,y=-2x+10;(2) 见解析;(3) B(4,3)
【解析】
(1)先求出k的值,进而得出mn=12,然后利用三角形的面积公式建立方程,联立方程组求解即可;
(2)先表示出BE,CE,DE,AE,进而求出BECE和DEAE即可得出结论;
(3)利用(2)的结论得出△DEC∽△BEA,进而得出AB∥CD,即可得出四边形ADCB是菱形即可得出点B的坐标.
(1)∵函数y=![]() (x>0,k是常数)的图象经过A(2,6),
(x>0,k是常数)的图象经过A(2,6),
∴k=2×6=12,
∵B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,
∴mn=12①,BD=m,AE=6-n,
∵△ABD的面积为3,
∴![]() BDAE=3,
BDAE=3,
∴![]() m(6-n)=3②,
m(6-n)=3②,
联立①②得,m=3,n=4,
∴B(3,4);
设直线AB的解析式为y=kx+b(k≠0),
则![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=-2x+10 ;
(2) ∵A(2,6),B(m,n),
∴BE=m-2,CE=n,DE=2,AE=6-n,
∴DEAE=2(6-n)=12-2n,
BECE=n(m-2)=mn-2n=12-2n,
∴DEAE=BECE,
∴![]() ;
;
(3) 由(2)知,![]() ,
,
∵∠AEB=∠DEC=90°,
∴△DEC∽△BEA,
∴∠CDE=∠ABE
∴AB∥CD,
∵AD∥BC,
∴四边形ADCB是平行四边形.
又∵AC⊥BD,
∴四边形ADCB是菱形,
∴DE=BE,CE=AE.
∴B(4,3).
故答案为:(1)![]() ,y= -2x+10;(2) 见解析;(3) B(4,3)
,y= -2x+10;(2) 见解析;(3) B(4,3)

 寒假学与练系列答案
寒假学与练系列答案