ƒøƒĞ»ı
°æƒø°ø“—÷™£∫µ„![]() ‘ĞÕ¨“ªÃ÷±œş…œ£¨µ„
‘ĞÕ¨“ªÃ÷±œş…œ£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£Æ
µƒ÷–µ„£Æ
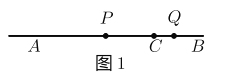
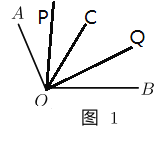
£®1£©»ÁÕº1 £¨µ±µ„![]() ‘Ğœş∂Œ
‘Ğœş∂Œ![]() …œ ±£Æ
…œ ±£Æ
¢Ÿ»Ù![]() £¨‘Úœş∂Œ
£¨‘Úœş∂Œ![]() µƒ≥§Œ™_______£Æ
µƒ≥§Œ™_______£Æ
¢Ğ»Ùµ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() …œ»Œ“‚“ªµ„£¨
…œ»Œ“‚“ªµ„£¨ ![]() £¨‘Úœş∂Œ
£¨‘Úœş∂Œ![]() µƒ≥§Œ™_______£Æ £® ”√∫¨
µƒ≥§Œ™_______£Æ £® ”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£©
µƒ¥˙ ˝ Ω±Ì æ£©
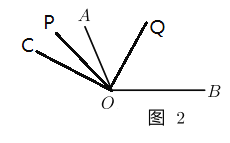
£®2£©»ÁÕº2 £¨µ±µ„![]() ≤ª‘Ğœş∂Œ
≤ª‘Ğœş∂Œ![]() …œ ±£¨»Ù
…œ ±£¨»Ù![]() £¨«Û
£¨«Û![]() µƒ≥§£®”√∫¨
µƒ≥§£®”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£© £Æ
µƒ¥˙ ˝ Ω±Ì æ£© £Æ
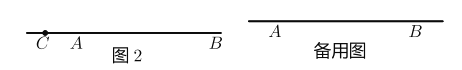
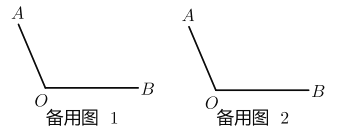
£®3£©»ÁÕº£¨“—÷™![]() £¨◊˜…‰œş
£¨◊˜…‰œş![]() £¨»Ù…‰œş
£¨»Ù…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]() £¨…‰œş
£¨…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]() £Æ
£Æ
¢Ÿµ±…‰œş![]() ‘Ğ
‘Ğ![]() µƒƒĞ≤ø ±£¨‘Ú
µƒƒĞ≤ø ±£¨‘Ú![]() =________°„£Æ
=________°„£Æ
¢Ğµ±…‰œş![]() ‘Ğ
‘Ğ ![]() µƒÕ‚≤ø ±£¨‘Ú
µƒÕ‚≤ø ±£¨‘Ú![]() =_______°„£Æ £® ”√∫¨
=_______°„£Æ £® ”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£© £Æ
µƒ¥˙ ˝ Ω±Ì æ£© £Æ
°æ¥∞∏°ø£®1£©¢Ÿ5£ª¢Ğ![]() £ª£®2£©
£ª£®2£© ![]() £ª£®3£©¢Ÿ
£ª£®3£©¢Ÿ![]() £ª¢Ğ
£ª¢Ğ![]() £Æ
£Æ
°æΩ‚Œˆ°ø
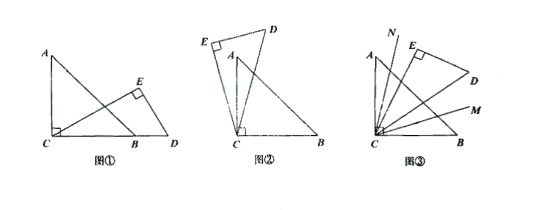
(1) ¢Ÿœ»«Û≥ˆPC=4,QC=1£¨‘Ÿ«Ûœş∂Œ![]() µƒ≥§º¥ø…£ª
µƒ≥§º¥ø…£ª
¢Ğœ»«Û≥ˆPC= ![]() AC,QC=
AC,QC=![]() BC£¨º¥ø…”√m±Ì æœş∂Œ
BC£¨º¥ø…”√m±Ì æœş∂Œ![]() µƒ≥§£ª
µƒ≥§£ª
(2) µ±µ„![]() ≤ª‘Ğœş∂Œ
≤ª‘Ğœş∂Œ![]() …œ ±£¨œ»«Û≥ˆPC=
…œ ±£¨œ»«Û≥ˆPC= ![]() AC,QC=
AC,QC=![]() BC£¨∏˘æıÕº–Œ”√m±Ì æœş∂Œ
BC£¨∏˘æıÕº–Œ”√m±Ì æœş∂Œ![]() µƒ≥§º¥ø…£ª
µƒ≥§º¥ø…£ª
(3)) ◊œ»∞¥’’“‚ª≠≥ˆÕº–Œ£¨∑÷OC‘Ğ°œAOBƒĞ≤ø∫ÕÕ‚≤ø¡Ω÷÷«Èøˆ£¨œ»«Û≥ˆ°œPOC= ![]() °œAOC,°œCOQ=
°œAOC,°œCOQ=![]() °œCOB£¨‘Ÿ∏˘æıÕº–Œ”√±Ì æ
°œCOB£¨‘Ÿ∏˘æıÕº–Œ”√±Ì æ![]() º¥ø…£Æ
º¥ø…£Æ
Ω‚£∫(1) ¢Ÿ°ş![]() £¨µ„
£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°‡PC=4,QC=1£¨
°‡PQ=PC+QC=5£¨
π ¥∞∏Œ™5£ª
¢Ğµ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() …œ»Œ“‚“ªµ„£¨
…œ»Œ“‚“ªµ„£¨ ![]() £¨µ„
£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°‡PC= ![]() AC,QC=
AC,QC=![]() BC£¨
BC£¨
°‡PQ=PC+QC=![]() AC+
AC+![]() BC=
BC=![]() AB=
AB=![]() m£¨
m£¨
π ¥∞∏Œ™![]() m.
m.
(2)µ±µ„C‘Ğœş∂ŒBAµƒ—”≥§œş ±£¨»ÁÕº2£∫
![]() £¨µ„
£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°‡PC= ![]() AC,QC=
AC,QC= ![]() BC£¨
BC£¨
°‡PQ=QC-PC=![]() BC-
BC-![]() AC=
AC=![]() AB=
AB=![]() m£¨
m£¨
µ±µ„C‘Ğœş∂ŒABµƒ—”≥§œş ±£¨»ÁÕº3£∫
![]() £¨µ„
£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™œş∂Œ
Œ™œş∂Œ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°‡PC= ![]() AC,QC=
AC,QC= ![]() BC£¨
BC£¨
°‡PQ=PC-QC=![]() AC-
AC-![]() BC=
BC=![]() AB=
AB=![]() m£¨
m£¨
°‡µ±µ„![]() ≤ª‘Ğœş∂Œ
≤ª‘Ğœş∂Œ![]() …œ ±£¨»Ù
…œ ±£¨»Ù![]() £¨
£¨ ![]() µƒ≥§Œ™
µƒ≥§Œ™![]() m.
m.
(3) ¢Ÿµ±…‰œş![]() ‘Ğ
‘Ğ![]() µƒƒĞ≤ø ±£¨»ÁÕº1£¨
µƒƒĞ≤ø ±£¨»ÁÕº1£¨
°ş…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]() £¨…‰œş
£¨…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]()
°‡°œPOC= ![]() °œAOC,°œCOQ=
°œAOC,°œCOQ=![]() °œCOB£¨
°œCOB£¨
°‡°œPOQ=°œPOC+°œCOQ= ![]() °œAOC+
°œAOC+![]() °œCOB =
°œCOB =![]() °œAOB=
°œAOB=![]() ,
,
π ¥∞∏Œ™![]() ;
;
¢Ğµ±…‰œş![]() ‘Ğ
‘Ğ ![]() µƒÕ‚≤ø ±£¨»ÁÕº2
µƒÕ‚≤ø ±£¨»ÁÕº2
°ş…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]() £¨…‰œş
£¨…‰œş![]() ∆Ω∑÷
∆Ω∑÷![]()
°‡°œPOC= ![]() °œAOC,°œCOQ=
°œAOC,°œCOQ=![]() °œCOB£¨
°œCOB£¨
°‡°œPOQ=°œQOC-°œCOP= ![]() °œCOB-
°œCOB-![]() °œAOC =
°œAOC =![]() °œAOB=
°œAOB=![]() ;
;
π ¥∞∏Œ™![]() .
.

 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏