题目内容
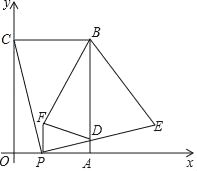
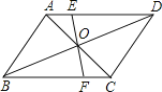
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.
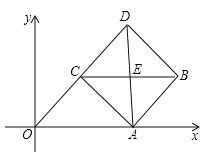
(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)利用平行四边形的性质及折叠的性质,可得出CD=AB,∠DCA=∠BAC,结合AC=CA可证出△ABC≌△CDA(SAS);
(2)由点D,C,O在同一直线上可得出∠DCA=∠OCA=90°,利用一次函数图象上点的坐标特征可得出点A的坐标及OA的长度,由OC∥AB可得出直线OC的解析式为y=x,进而可得出∠COA=45°,结合∠OCA=90°可得出△AOC为等腰直角三角形,利用等腰直角三角形的性质可得出OC、AC的长,结合(1)的结论可得出四边形ABDC为正方形,再利用正方形的面积公式结合S△ACE=![]() S正方形ABDC可求出△ACE的面积.
S正方形ABDC可求出△ACE的面积.
(1)证明:∵四边形ABCO为平行四边形,
∴AB=CO,AB∥OC,
∴∠BAC=∠OCA.
由折叠可知:CD=CO,∠DCA=∠OCA,
∴CD=AB,∠DCA=∠BAC.
在△ABC和△CDA中,
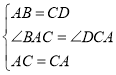 ,
,
∴△ABC≌△CDA(SAS).
(2)解:∵∠DCA=∠OCA,点D,C,O在同一直线上,
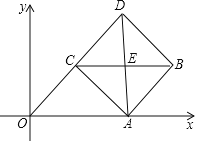
∴∠DCA=∠OCA=90°.
当y=0时,x-6=0,解得:x=6,
∴点A的坐标为(6,0),OA=6.
∵OC∥AB,
∴直线OC的解析式为y=x,
∴∠COA=45°,
∴△AOC为等腰直角三角形,
∴AC=OC=![]() .
.
∵AB∥CD,AB=CD=AC,∠DCA=90°,
∴四边形ABDC为正方形,
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目