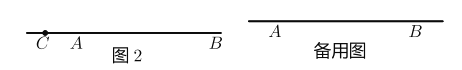��Ŀ����
����Ŀ����ͼ �������ᣮ����![]() �����㣨��
�����㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ ��
����ࣩ �� ![]()
![]()
��1�������![]() ��ʾ������
��ʾ������![]() ����ô��
����ô��
�ٵ�![]() ��ʾ������_______��
��ʾ������_______��
�������![]() �ӵ�
�ӵ�![]() �������������������˶����ٶ���ÿ��3����λ���ȣ��˶����
�������������������˶����ٶ���ÿ��3����λ���ȣ��˶����![]() ��ʾ������_______���� �ú�
��ʾ������_______���� �ú�![]() �Ĵ���ʽ��ʾ�� �� ����________�� ��
�Ĵ���ʽ��ʾ�� �� ����________�� �� ![]() ��
��
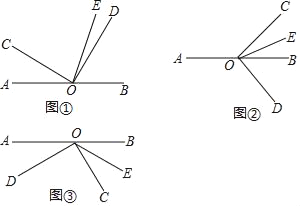
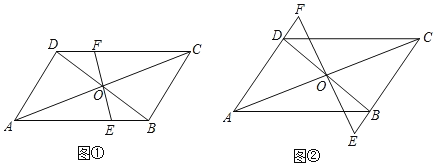
��2�������![]() ��ʾ������
��ʾ������![]() ��������ĸ�������ԭ��
��������ĸ�������ԭ��![]() ˳ʱ����ת60�� ���õ�
˳ʱ����ת60�� ���õ�![]() ����ͼ2��ʾ������
����ͼ2��ʾ������![]() ��
��![]() �����Ƶ�
�����Ƶ�![]() ˳ʱ����ת���ٶ���ÿ��15�� ��ͬʱ������
˳ʱ����ת���ٶ���ÿ��15�� ��ͬʱ������![]() ��
��![]() �����Ƶ�
�����Ƶ�![]() ��ʱ����ת���ٶ���ÿ��5�� �����˶�ʱ��Ϊ
��ʱ����ת���ٶ���ÿ��5�� �����˶�ʱ��Ϊ![]() �룬��
�룬��![]() ��ʱ��
��ʱ�� ![]() ֹͣ�˶���
ֹͣ�˶���
�ٵ�![]() Ϊ________��ʱ��
Ϊ________��ʱ��![]() ��
��![]() �غϣ�
�غϣ�
�ڵ�![]() ʱ��
ʱ��![]() ��ֵ��________��
��ֵ��________��

���𰸡���1����15����![]() ��
��![]() ����2����6����
����2����6����![]() ��
��![]() ��
��
��������
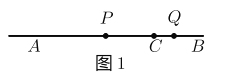
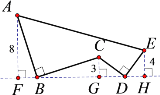
(1) ��)������֪�ɵ�B���ʾ����Ϊ15��
�ڵ�![]() �ӵ�
�ӵ�![]() �������ٶ���ÿ��3����λ���ȣ��ɵõ�
�������ٶ���ÿ��3����λ���ȣ��ɵõ�![]() ��ʾ������
��ʾ������![]() ������t�룬CA=3t,CB=20-3t,���������з�����⼴�ɣ�
������t�룬CA=3t,CB=20-3t,���������з�����⼴�ɣ�
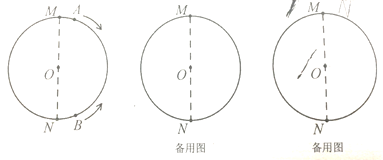
��2�������˶�ʱ��Ϊ![]() ��, OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ��������з�����⼴�ɣ�
��, OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ��������з�����⼴�ɣ�
�ڷֵ���P��OB����ʱ�͵���P��OB����ʱ���������з�����⼴��.
�⣺(1) �١ߵ�![]() ��ʾ������
��ʾ������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����࣬
����࣬
�������ϵ�B��ʾ����Ϊ15��
�ʴ�Ϊ15��
�ڡߵ�![]() �ӵ�
�ӵ�![]() �������������������˶����ٶ���ÿ��3����λ���ȣ�
�������������������˶����ٶ���ÿ��3����λ���ȣ�
���![]() ��ʾ������3t-5;
��ʾ������3t-5;
����t�룬CA=3t,CB=20-3t,
��CA=CB,
��3t=20-3t,
��ã�t=![]() ,
,
�ʴ�Ϊ3t-5��![]() .
.
(2) �����˶�ʱ��Ϊ![]() ��, OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ�������ã�
��, OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ�������ã�
15t+5t=120,
��ã�t=6,
�ʴ�Ϊ6��
�ڵ���P��OB����ʱ��OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ�
��![]() =120��-��15t������
=120��-��15t������![]() =(5t)������������ã�
=(5t)������������ã�
120-15t=![]() ��5t,
��5t,
��ã�t=![]()
����P��OB����ʱ��OP��ת�ĽǶ�Ϊ15t�ȣ�OQ��ת�ĽǶ�Ϊ5t�ȣ�
��![]() =��15t����-120�㣬
=��15t����-120�㣬![]() =(5t)�㣬��������ã�
=(5t)�㣬��������ã�
15t-120=![]() ��5t,
��5t,
��ã�t=![]() ,
,
�ʴ�Ϊ![]() ��
��![]() .
.

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�