题目内容
【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
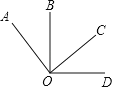
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
【答案】(1)∠AOB=30°,∠DOC=30°;(2)∠COD=30°;(3)当α=45°时,∠AOD与∠BOC互余.
【解析】
(1)根据互余的意义,即可求出答案;
(2)设出未知数,利用题目条件,表示出∠AOB、∠BOC,进而列方程求解即可;
(3)利用角度的和与差,反推得出结论,再利用互余得出答案.
(1)∵∠AOC=90°,∠BOD=90°,∠BOC=60°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°,
∠DOC=∠BOD﹣∠BOC=90°﹣60°=30°;
(2)设∠COD=x°,则∠BOC=100°﹣x°.
∵∠AOC=110°,
∴∠AOB=110°﹣(100°﹣x°)=x°+10°.
∵∠AOD=∠BOC+70°,
∴100°+10°+x°=100°﹣x°+70°,
解得:x=30,
即∠COD=30°;
(3)当α=45°时,∠AOD与∠BOC互余.理由如下:
要使∠AOD与∠BOC互余,即∠AOD+∠BOC=90°,
∴∠AOB+∠BOC+∠COD+∠BOC=90°,
即∠AOC+∠BOD=90°.
∵∠AOC=∠BOD=α,
∴∠AOC=∠BOD=45°,
即α=45°,
∴当α=45°时,∠AOD与∠BOC互余.


练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目