Question

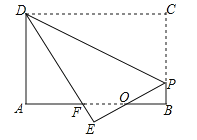
【题目】如图，矩形纸片ABCD，AB=4，BC=3，点P在BC边上，将△CDP沿DP折叠，点C落在点E处，PE、DE分别交AB于点O、F，且OP=OF，则的值为（ ）.

A. B. C. D.

Answer 1

【答案】C

【解析】

根据折叠的性质可得出DC=DE、CP=EP，由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP（AAS），根据全等三角形的性质可得出OE=OB、EF=BP，设EF=x，则BP=x、DF=4﹣x、BF=PC=3﹣x，进而可得出AF=1+x．在Rt△DAF中，利用勾股定理可求出x的值，即可得出答案．

根据折叠，可知：△DCP≌△DEP，∴DC=DE=4，CP=EP．

在△OEF和△OBP中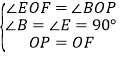，∵，∴△OEF≌△OBP（AAS），∴OE=OB，EF=BP．

设EF=x，则BP=x，DF=DE﹣EF=4﹣x．

又∵BF=OB+OF=OE+OP=PE=PC，PC=BC﹣BP=3﹣x，∴AF=AB﹣BF=1+x．

在Rt△DAF中，AF2+AD2=DF2，即（1+x）2+32=（4﹣x）2，解得：x=0.6，∴DF=4﹣x=3.4，∴．

故选C．