题目内容
【题目】已知，直线l1：y=﹣x+n过点A（﹣1，3），双曲线C：y= 
（x＞0），过点B（1，2），动直线l2：y=kx﹣2k+2（常数k＜0）恒过定点F．
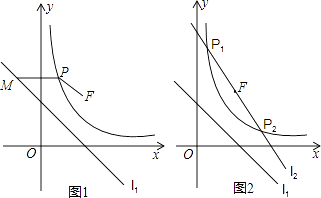
（1）求直线l1 ， 双曲线C的解析式，定点F的坐标；
（2）在双曲线C上取一点P（x，y），过P作x轴的平行线交直线l1于M，连接PF．求证：PF=PM．
（3）若动直线l2与双曲线C交于P1 ， P2两点，连接OF交直线l1于点E，连接P1E，P2E，求证：EF平分∠P1EP2 ．
【答案】
（1）解：∵直线l1：y=﹣x+n过点A（﹣1，3），
∴﹣（﹣1）+n=3，
解得：n=2，
∴直线l1的解析式为：y=﹣x+2，
∵双曲线C：y= 
（x＞0）过点B（1，2），
∴m=xy=1×2=2，
即双曲线C的解析式为：y= 
，
∵动直线l2：y=kx﹣2k+2=k（x﹣2）+2，
∴不论k为任何负数时，当x=2时，则y=2，
即动直线l2：y=kx﹣2k+2恒过定点F（2，2）
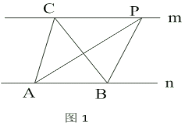
（2）证明：如图1，在双曲线C上任取一点P（x，y），过P作x轴的平行线交直线l1于M（x0，y），连接PF．
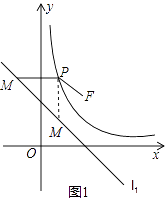
则PF=x﹣x0，
又∵M（x0，y）在直线l1上，
∴﹣x0+2=y，
∴x0=2﹣y=2﹣ ，
∴PM=x+ ﹣2，
又∵PF= 
= 
= 
= 
=x+ ﹣2；
（注：x+ ﹣2=（ 
）2+（ 
）2﹣2 +2 
﹣2=（ ﹣ ）2+2 ﹣2=（ ﹣ ）2+2（ ﹣1）≥2（ ﹣1）＞0）
∴PM=PF；
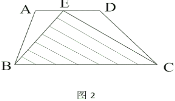
（3）证明：证明：如图2，过P1分别作P1M1∥x轴交l1于M1，作P1N1⊥l1，垂足为N1，过P2分别作P2M2∥x轴交l1于M2，作P2N2⊥l1，垂足为N2，
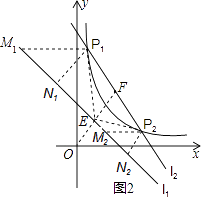
∵直线l1的解析式为y=﹣x+2，
∴△P1M1N1和△P2M2N2都是等腰直角三角形．
∴P1N1= 
P1M1= P1F，P2N2= P2M2= P2F，
∵直线EF的解析为：y=x，
∴EF⊥l1，
∴P1N1∥EF∥P2N2，
∴ 
= 
= 
，
即 
= ，
∴△P1N1E∽△P2N2E，
∴∠P1EN1=∠P2EN2，
∵∠P1EF=90°﹣∠P1EN1，∠P2EF=90°﹣∠P2EN2，
∴∠P1EF=∠P2EF，
∴EF平分∠P1EP2．
【解析】（1）由直线l1：y=﹣x+n过点A（﹣1，3），双曲线C：y= （x＞0），过点B（1，2），利用待定系数法即可求得直线l1，双曲线C的解析式；由动直线l2：y=kx﹣2k+2，配方法可求得定点F的坐标；（2）首先在双曲线C上任取一点P（x，y），过P作x轴的平行线交直线l1于M（x0，y），连接PF．然后分别求得PM与PF的长，继而证得结论；（3）首先过P1分别作P1M1∥x轴交l1于M1，作P1N1⊥l1，垂足为N1，过P2分别作P2M2∥x轴交l1于M2，作P2N2⊥l1，垂足为N2，易证得EF⊥l1，可得P1N1∥EF∥P2N2，继而证得△P1N1E∽△P2N2E，然后由相似三角形的对应角相等，证得结论．
