题目内容
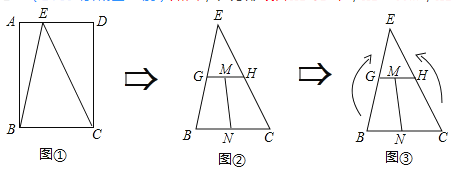
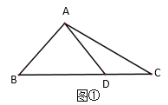
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
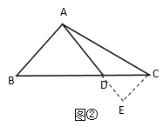
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
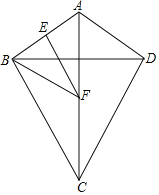
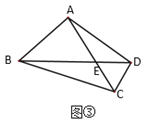
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
【答案】【问题探究】(1)![]() ;(2)
;(2)![]() .【拓展应用】
.【拓展应用】![]() .
.
【解析】
问题探究:
(1)由平行线的性质得出∠ACE+∠BAC=180°,即可得出结果;
(2)由平行线的性质得出∠E=∠BAD=72°,证出AC=AE,由平行线证明△ABD∽△ECD,求出AD=2;ED=4,ED=2,得出AC=AE=AD+ED=6;
拓展应用:过点D作DF∥AB交AC于点F.证明△BAE∽△DFE,得出![]() =2,得出AB=2DF,EF=
=2,得出AB=2DF,EF=![]() AE=1,AF=AE+EF=3,证出AC=AD,在Rt△ADF中,求出DF=AF×tan∠CAD=
AE=1,AF=AE+EF=3,证出AC=AD,在Rt△ADF中,求出DF=AF×tan∠CAD=![]() ,得出AC=AD=2DF=2
,得出AC=AD=2DF=2![]() ,AB=2DF=2
,AB=2DF=2![]() ,得出AC=AB,在Rt△ABC中,求出BC=
,得出AC=AB,在Rt△ABC中,求出BC=![]() AB=2
AB=2![]() 即可.
即可.
解:(1)∵CE∥AB,
∴∠ACE+∠BAC=180°,
∴∠ACE=180°-108°=72°;
故答案为:72;
(2)∵CE∥AB,
∴∠E=∠BAD=72°,
∴∠E=∠ACE,
∴AC=AE,
∵CE∥AB,
∴△ABD∽△ECD,
∴![]() ,
,
∵BD=2CD,
∴![]() =2,
=2,
∴AD=2ED=4,
∴ED=2,
∴AC=AE=AD+ED=4+2=6;

拓展应用:
解:如图3中,过点D作DF∥AB交AC于点F.
∵AC⊥AB,∴∠BAC=90°,∵DF∥AB,
∴∠DFA=∠BAC=90°,
∵∠AEB=∠DEF,
∴△BAE∽△DFE,
∴![]() =2,
=2,
∴AB=2DF,EF=![]() AE=1,AF=AE+EF=3,
AE=1,AF=AE+EF=3,
∵∠BAD=120°,
∴∠CAD=30°,
∴∠ACD=75°=∠ADC,
∴AC=AD,
在Rt△ADF中,∵∠CAD=30°,
∴DF=AF×tan∠CAD3×![]() ,
,
∴AC=AD=2DF=2![]() ,AB=2DF=2
,AB=2DF=2![]() ,
,
∴AC=AB,
在Rt△ABC中,∵∠BAC=90°,
∴BC=![]() AB=2
AB=2![]() ;
;
故答案为:2![]() .
.

 阅读快车系列答案
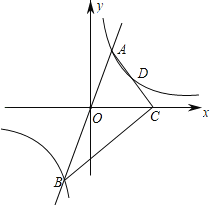
阅读快车系列答案【题目】已知抛物线y=-x2-2x+c与x轴的一个交点是(1,0).
(1)C的值为_______;
(2)选取适当的数据补填下表,并在平面直角坐标系内描点画出该抛物线的图像;
|
|
|
|
| |||
|
|
|
|
(3)根据所画图像,写出y>0时x的取值范围是_____.