题目内容
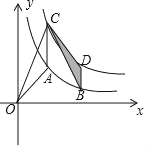
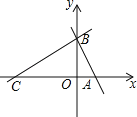
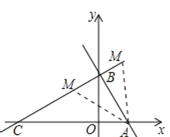
【题目】如图,平面直角坐标系中,直线y=﹣![]() x+
x+![]() 与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2.
与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2.
(1)求A、C两点的坐标;
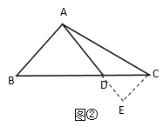
(2)若点M从点C出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
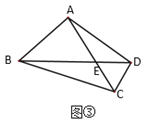
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点,且以AB为边的四边形是菱形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)C(﹣3,0);(2)S=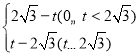 ;(3)存在,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0)
;(3)存在,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0)
【解析】
(1)求出A,B两点的坐标,求出AB=2,则OC可求出,则点C的坐标可求出;
(2)先求出∠ABC=90°,分两种情况考虑:当M在线段BC上;当M在线段BC延长线上;表示出BM,利用三角形面积公式分别表示出S与t的函数关系式即可;
(3)点P是y轴上的点,在坐标平面内存在点Q,使以A、B、P、Q为顶点的四边形是菱形,如图所示,利用菱形的性质,根据AQ与y轴平行或垂直,求出满足题意Q得坐标即可.
解:(1)对于直线y=﹣![]() x+
x+![]() ,
,
当y=0 时,![]() =0,
=0,
解得:x=1,
∴A(1,0),
∴OA=1,
当x=0 时,y=![]() ,
,
∴B(0,![]() ),
),
∴OB=![]() ,
,
∵∠AOB=90°,
∴AB=![]() =
=![]() =2,
=2,
∵AB:AC=1:2,
∴AC=4,
∴OC=3,
∴C(﹣3,0);
(2)如图所示,
∵![]() ,
,![]() ,
,![]() ,
,
∴∠ABO=30°,
同理:BC=2![]() ,∠OCB=30°,
,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:
①若M在线段BC上时,
BC=2![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2![]() ﹣t,
﹣t,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(2
×(2![]() ﹣t)×2=2
﹣t)×2=2![]() ﹣t(0≤t<2
﹣t(0≤t<2![]() );
);
②若M在BC延长线上时,BC=2![]() ,CM=t,
,CM=t,
可得BM=CM﹣BC=t﹣2![]() ,
,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(t﹣2
×(t﹣2![]() )×2=t﹣2
)×2=t﹣2![]() (t≥2
(t≥2![]() );
);
综上所述,S=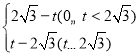 ;
;
(3)存在.若AB是菱形的边,如下图所示,
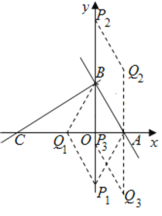
在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),
在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),
在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),
综上,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0).

【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?