题目内容
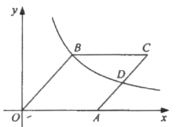
【题目】如图,过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
(k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
【答案】C
【解析】
设A(t,![]() ),然后再利用线段的中点坐标公式得到D点坐标,则
),然后再利用线段的中点坐标公式得到D点坐标,则![]() ,解得t=1,所以A(1,k);再证明OC为Rt△ACB斜边上的中线,则OA=OC=3,最后利用勾股定理列方程解答即可.
,解得t=1,所以A(1,k);再证明OC为Rt△ACB斜边上的中线,则OA=OC=3,最后利用勾股定理列方程解答即可.
解:设A(t,![]() ),
),
∵C(3,0),AD=CD,
∴D点坐标为(![]() ,
,![]() ),
),
∵点D在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴![]() ,解得t=1,
,解得t=1,
∴A(1,k),
∵AC⊥BC,
∴∠ACB=90°,
∵过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,
(k>0)的图象交于点A,B两点,
∴点A与点B关于原点对称,即OA=OB,
∴OC=OA=OB=3,
∴12+k2=32,解得k=2![]() .
.
故选C.

练习册系列答案
相关题目
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
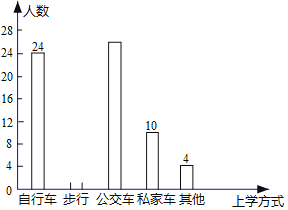
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.