题目内容
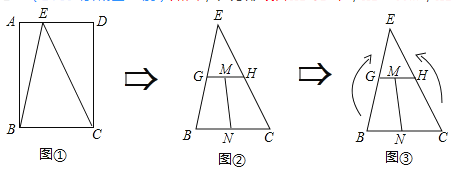
【题目】如图，矩形纸片ABCD中，AB=8cm，AD=6cm，按下列步骤进行裁剪和拼图：
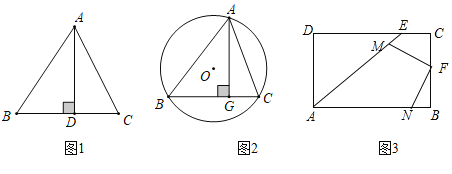
第一步：如图①，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC（余下部分不再使用）；
第二步：如图②，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；
第三步：如图③，将MN左侧纸片绕G点按顺时针旋转180，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180，使线段HC与HE重合，拼成一个与三角形纸片EBC面积相等的四边形纸片（裁剪和拼图过程均无缝且不重叠）则拼成的这个四边形纸片的周长的最大值为___cm．
【答案】
【解析】
首先确定剪拼之后的四边形是个平行四边形，其周长大小取决于MN的大小．然后在矩形中探究MN的不同位置关系，得到其长度的最大值与最大值，从而问题解决．
解：画出第三步剪拼之后的四边形M1N1N2M2的示意图，如答图1所示．
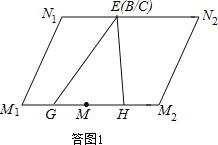
图中，N1N2=EN1+EN2=NB+NC=BC，
M1M2=M1G+GM+MH+M2H=2（GM+MH）=2GH=BC（三角形中位线定理），
又∵M1M2∥N1N2，
∴四边形M1N1N2M2是一个平行四边形，
其周长为2N1N2+2M1N1=2BC+2MN．
∵BC=6为定值，
∴四边形的周长取决于MN的大小．
如答图2所示，是剪拼之前的完整示意图，
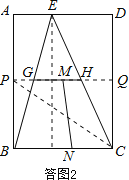
过G、H点作BC边的平行线，分别交AB、CD于P点、Q点，则四边形PBCQ是一个矩形，这个矩形是矩形ABCD的一半，
∵M是线段PQ上的任意一点，N是线段BC上的任意一点，
根据垂线段最短，得到MN的最小值为PQ与BC平行线之间的距离，即MN最小值为4；
而MN的最大值等于矩形对角线的长度，即
，
四边形M1N1N2M2的周长=2BC+2MN=12+2MN，
∴最大值为12+2×
=12+
．
故答案为：12+．
