题目内容
【题目】综合与探究:
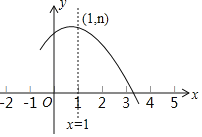
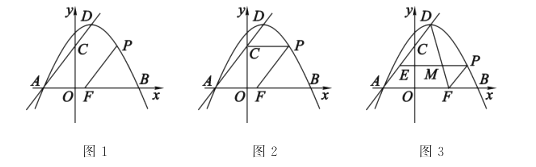
如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() ,
,![]() 为对称轴右侧抛物线的一个动点,直线
为对称轴右侧抛物线的一个动点,直线![]() 与
与![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的函数表达式及点
的函数表达式及点![]() 的坐标;
的坐标;
(2)如图2,当![]() 轴时,将
轴时,将![]() 以每秒1个单位长度的速度沿
以每秒1个单位长度的速度沿![]() 轴的正方向平移,当点
轴的正方向平移,当点![]() 与点
与点![]() 重合时停止平移.设平移
重合时停止平移.设平移![]() 秒时,在平移过程中
秒时,在平移过程中![]() 与四边形
与四边形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
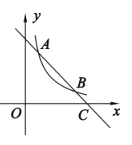
(3)如图3,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②试探究点![]() 在运动过程中,是否存在值
在运动过程中,是否存在值![]() ,使四边形
,使四边形![]() 是菱形?若存在,请直接写出点
是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)①
;(3)①![]() 或
或![]() ,②
,②![]()
【解析】
(1)先通过抛物线函数关系式求出与x轴的两个交点A、B的坐标以及顶点D的坐标,再利用待定系数可求得直线AD的函数表达式,令x=0,即可求得点C的坐标;
(2)先求出点P坐标![]() ,通过平移可求得
,通过平移可求得![]() ,从而可得OF的长为
,从而可得OF的长为![]() ,当
,当![]() 时,重叠部分为△AOC,求出△AOC的面积即可,当
时,重叠部分为△AOC,求出△AOC的面积即可,当![]() 时,
时,![]() 平移
平移![]() 秒到
秒到![]() 的位置,
的位置,![]() 交
交![]() 于点
于点![]() ,如图,重叠部分为四边形
,如图,重叠部分为四边形![]() ,根据
,根据![]() 结合相似三角形的性质可表示出
结合相似三角形的性质可表示出![]() 的长,再根据四边形
的长,再根据四边形![]() 的面积=
的面积=![]() 的面积-
的面积-![]() 的面积即可求出
的面积即可求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)①过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,利用点P、D的坐标表示出DN、NQ的长,再根据平行得
,利用点P、D的坐标表示出DN、NQ的长,再根据平行得![]() ,结合
,结合![]() 列出方程求解即可;
列出方程求解即可;
②当点P在第一象限时,过点P作PG⊥x轴于点G,易证△PGF∽△COA,故可设PG=4k,FG=3k,由勾股定理得PF=5k,由菱形得AF=PF=5k,故可表示出点P坐标,将点P坐标代入抛物线函数关系式列出方程求解即可,当点P在第四象限时,同理可得点P坐标.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∵点![]() 在点
在点![]() 的左侧,
的左侧,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() .
.
(2)当![]() 时,
时,![]() ,
,
解得:![]() ,
,
∵点![]() 在抛物线对称轴的右侧,
在抛物线对称轴的右侧,
∴ ![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
当![]() 时,
时,![]() 平移
平移![]() 秒到
秒到![]() 的位置,
的位置,![]() 交
交![]() 于点
于点![]() ,如图,
,如图,
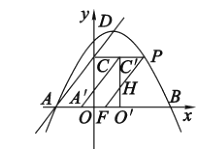
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即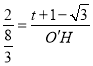 ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
=![]()
![]() .
.
综上所述,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
(3)①如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
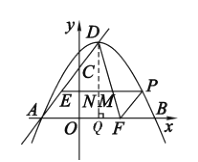
∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,
![]() ,
,
∵点![]() 在抛物线对称轴的右侧,
在抛物线对称轴的右侧,
∴![]() ;
;
当![]() 时,
时,
![]() ,
,
∵点![]() 在抛物线对称轴的右侧,
在抛物线对称轴的右侧,
∴![]() ,
,
综上所述,![]() 或
或![]() ,
,
②如图,当点P在第一象限时,过点P作PG⊥x轴于点G,
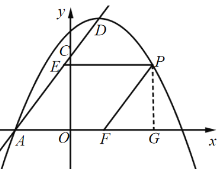
∵PF∥AC,
∴∠PFG=∠CAO
又∵∠PGF=∠COA=90°,
∴△PGF∽△COA,
∴![]() ,
,
∴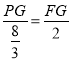 ,
,
∴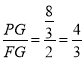 ,
,
∴设PG=4k,FG=3k,则PF=5k,
∵四边形![]() 是菱形
是菱形
∴AF=PF=5k,
又∵点A(-2,0),
∴点P(-2+8k,4k)
∵点P在抛物线![]() 的图像上,
的图像上,
∴![]() ,
,
整理得![]()
解得![]() (舍去)
(舍去)
∴![]()
∴点P的坐标为![]() ,
,
如图,当点P在第四象限时,过点P作PK⊥x轴于点K,
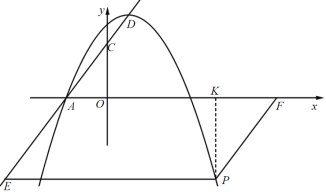
∵PF∥AC,
∴∠PFK=∠CAO,
又∵∠PKF=∠COA=90°,
∴△PKF∽△COA,
∴![]() ,
,
∴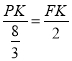 ,
,
∴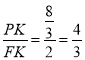 ,
,
∴设PK=4a,FK=3a,则PF=5a,
∵四边形![]() 是菱形
是菱形
∴AF=PF=5a,
又∵点A(-2,0),
∴点P(-2+2a,-4a)
∵点P在抛物线![]() 的图像上,
的图像上,
∴![]() ,
,
整理得![]()
解得![]() (舍去)
(舍去)
∴![]()
∴点P的坐标为![]() ,
,
综上所述,存在![]() ,使四边形
,使四边形![]() 是菱形,此时点
是菱形,此时点![]() 的坐标为
的坐标为![]() .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案