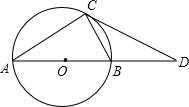
题目内容
如图，AB为⊙O的弦，若OA⊥OD且CD=BD．求证：BD是⊙O的切线．
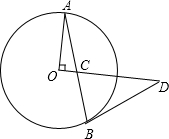
证明：连接OB，
∵OA=OB，CD=DB，
∴∠OAC=∠OBC，∠DCB=∠DBC．
∵∠OAC+∠ACO=90°，∠ACO=∠DCB，
∴∠OBC+∠DBC=90°．
∴OB⊥BD．
即BD是⊙O的切线．
∵OA=OB，CD=DB，
∴∠OAC=∠OBC，∠DCB=∠DBC．
∵∠OAC+∠ACO=90°，∠ACO=∠DCB，
∴∠OBC+∠DBC=90°．
∴OB⊥BD．
即BD是⊙O的切线．
练习册系列答案
相关题目
45°．
