ЬтФПФкШн
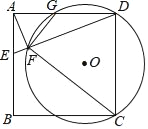
ЁОЬтФПЁПвбжЊЃЌШчЭМЫљЪОЃЌдкОиаЮABCDжаЃЌЕуEдкBCБпЩЯЃЌЁїAEFЃН90Ёу
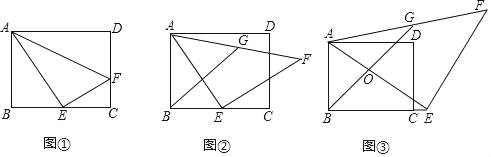
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊЕуFдкCDБпЩЯЃЌADЃНAEЃН5ЃЌABЃН4ЃЌЧѓDFЕФГЄЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌвбжЊAEЃНEFЃЌGЮЊAFЕФжаЕуЃЌЪдЬНОПЯпЖЮABЃЌBEЃЌBGЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌЕуEдкОиаЮABCDЕФBCБпЕФбгГЄЯпЩЯЃЌAEгыBGЯрНЛгкOЕуЃЌЦфЫћЬѕМўгыЃЈ2ЃЉБЃГжВЛБфЃЌADЃН5ЃЌABЃН4ЃЌCEЃН1ЃЌЧѓЁїAOGЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉAB+BEЃН
ЃЛЃЈ2ЃЉAB+BEЃН![]() BGЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉ
BGЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнОиаЮаджЪЧѓГіAE,дЫгУЙДЙЩЖЈРэЧѓBE,EC,дйжЄRtЁїAEFЁеRtЁїADFЃЈHLЃЉЃЌдкRtЁїCEFжаЃЌгЩЙДЙЩЖЈРэЕУНсЙћЃЛЃЈ2ЃЉзїFMЁЭBCНЛBCЕФбгГЄЯпгкMЃЌзїGNЁЭBCгкNЃЌСЌНгGMЃЌЁїABEЁеЁїEMFЃЈAASЃЉЃЌЕУABЃНEMЃЌBEЃНFMЃЌжЄЕуNЮЊBMЕФжаЕуЃЌGNЃН![]() ЃЈAB+FMЃЉЃЌдйНтжБНЧШ§НЧаЮПЩЕУЃЛЃЈ3ЃЉСЌНгEGЃЌзїOPЁЭBEгкPЃЌзїOQЁЭAGгкQЃЌИљОнОиаЮаджЪЃЌжЄГіЕШбќжБНЧШ§НЧаЮЃЌдйНтжБНЧШ§НЧаЮЃЌЧѓГіЙиМќЯпЖЮГЄЖШЃЌдйЧѓУцЛ§.
ЃЈAB+FMЃЉЃЌдйНтжБНЧШ§НЧаЮПЩЕУЃЛЃЈ3ЃЉСЌНгEGЃЌзїOPЁЭBEгкPЃЌзїOQЁЭAGгкQЃЌИљОнОиаЮаджЪЃЌжЄГіЕШбќжБНЧШ§НЧаЮЃЌдйНтжБНЧШ§НЧаЮЃЌЧѓГіЙиМќЯпЖЮГЄЖШЃЌдйЧѓУцЛ§.
ЃЈ1ЃЉЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯAЃНЁЯCЃНЁЯDЃН90ЁуЃЌCDЃНABЃН4ЃЌ
ЁпADЃНAEЃЌADЃН5ЃЌ
ЁрAEЃН5ЃЌ
дкRtЁїABEжаЃЌгЩЙДЙЩЖЈРэЕУЃЌBEЃН![]() ЃН3ЃЌ
ЃН3ЃЌ
ЁрECЃН2ЃЌ
дкRtЁїAEFКЭRtЁїADFжаЃЌ![]() ЃЌ
ЃЌ
ЁрRtЁїAEFЁеRtЁїADFЃЈHLЃЉЃЌ
ЁрEFЃНDFЃЌ
ЩшDFЃНEFЃНxЃЌдђCFЃН4ЉxЃЌ
дкRtЁїCEFжаЃЌгЩЙДЙЩЖЈРэЕУЃК22+ЃЈ4ЉxЃЉ2ЃНx2ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
МДDFЕФГЄЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉAB+BEЃН![]() BGЃЎРэгЩШчЯТЃК
BGЃЎРэгЩШчЯТЃК
зїFMЁЭBCНЛBCЕФбгГЄЯпгкMЃЌзїGNЁЭBCгкNЃЌСЌНгGMЃЌШчЭМЂкЫљЪОЃК
дкЁїABEКЭЁїEMFжаЃЌ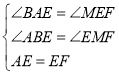 ЃЌ
ЃЌ
ЁрЁїABEЁеЁїEMFЃЈAASЃЉ
ЁрABЃНEMЃЌBEЃНFMЃЌ
ЁпABЁЭBCЃЌFMЁЭBCЃЌGNЁЭBCЃЌ
ЁрABЁЮGNЁЮFMЃЌгжЕуGЮЊAFЕФжаЕуЃЌ
ЁрЕуNЮЊBMЕФжаЕуЃЌGNЃН![]() ЃЈAB+FMЃЉЃЌ
ЃЈAB+FMЃЉЃЌ
ЁрGNЃН![]() BMЃЌ
BMЃЌ
ЁрGBЃНGNЃЌЁЯBGMЃН90ЁуЃЌ
ЁрBMЃН![]() BGЃЌ
BGЃЌ
ЁрAB+BEЃН![]() BGЃЎ
BGЃЎ
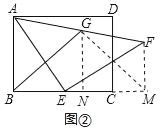
ЃЈ3ЃЉСЌНгEGЃЌзїOPЁЭBEгкPЃЌзїOQЁЭAGгкQЃЌШчЭМЂлЫљЪОЃК
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрBCЃНADЃН5ЃЌЁЯABCЃН90ЁуЃЌ
ЁрBEЃНBC+CEЃН6ЃЌ
ЁрAEЃН![]()
ЁпЁїAEFЪЧЕШбќжБНЧШ§НЧаЮЃЌGЪЧAFЕФжаЕуЃЌ
ЁрЁЯGAEЃН45ЁуЃЌEGЁЭAFЃЌ
ЁрЁїAGEЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯAGEЃН90ЁуЃЌ
ЁрAEЃН![]() AGЃЌ
AGЃЌ
ЁрAGЃН![]() ЃЌ
ЃЌ
ЁпЁЯABEЃН90ЁуЃЌ
ЁрЁЯABE+ЁЯAGEЃН180ЁуЃЌ
ЁрAЁЂBЁЂEЁЂGЫФЕуЙВдВЃЌ
ЁрЁЯGBEЃНЁЯGAEЃН45ЁуЃЌ
ЁрЁїOBPЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрOPЃНBPЃЌ
ЩшOPЃНBPЃНxЃЌ
ЁпtanЁЯAEBЃН![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЁрPEЃН![]() xЃЌ
xЃЌ
ЁпBP+PEЃНBEЃН6ЃЌ
Ёрx+![]() xЃН6ЃЌ
xЃН6ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
ЁрOPЃН![]() ЃЌ
ЃЌ
ЁрOEЃН![]() ЃЌ
ЃЌ
ЁрAOЃНAEЉOEЃН![]() ЃЌ
ЃЌ
дкRtЁїAOQжаЃЌЁЯOAQЃН45ЁуЃЌ
ЁрOQЃН![]() ЃЌ
ЃЌ
ЁрЁїAOGЕФУцЛ§ЃН![]() ЃЎ
ЃЎ

 ШЋФмВтПиЦкФЉаЁзДдЊЯЕСаД№АИ
ШЋФмВтПиЦкФЉаЁзДдЊЯЕСаД№АИЁОЬтФПЁПФГаЃОХФъМЖАЫИіАрЙВга280УћбЇЩњЃЌФаХЎЩњШЫЪ§ДѓжТЯрЭЌЃЌЕїВщаЁзщЮЊЕїВщбЇЩњЕФЬхжЪНЁПЕЫЎЦНЃЌПЊеЙСЫвЛДЮЕїВщбаОПЃЌЧыНЋЯТУцЕФЙ§ГЬВЙШЋ.
ЪеМЏЪ§ОнЃК
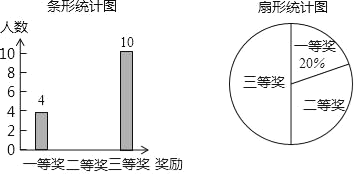
(1)ЕїВщаЁзщМЦЛЎбЁШЁ40УћбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈзїЮЊбљБОЃЌЯТУцЕФШЁбљЗНЗЈжаЃЌКЯРэЕФЪЧ___________ЃЈЬюзжФИЃЉЃЛ
AЃЎГщШЁОХФъМЖ1АрЁЂ2АрИї20УћбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈзщГЩбљБО
BЃЎГщШЁИїАрЬхг§ГЩМЈНЯКУЕФбЇЩњЙВ40УћбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈзщГЩбљБО
CЃЎДгФъМЖжаАДбЇКХЫцЛњбЁШЁФаХЎЩњИї20УћбЇЩњбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈзщГЩбљБО
ећРэЁЂУшЪіЪ§ОнЃК
ГщбљЗНЗЈШЗЖЈКѓЃЌЕїВщаЁзщЛёЕУСЫ40УћбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈШчЯТЃК
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
ећРэЪ§ОнЃЌШчЯТБэЫљЪОЃК
2018ФъОХФъМЖВПЗжбЇЩњбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈЭГМЦБэ
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
ЗжЮіЪ§ОнЁЂЕУГіНсТл
ЕїВщаЁзщНЋЭГМЦКѓЕФЪ§ОнгыШЅФъЭЌЦкОХФъМЖЕФбЇЩњЕФЬхжЪНЁПЕВтЪдГЩМЈЃЈжБЗНЭМЃЉНјааСЫЖдБШЃЌ
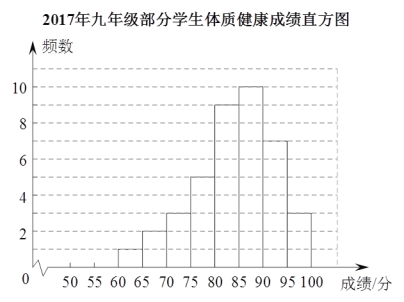
(2)ФуФмДгжаЕУЕНЕФНсТлЪЧ_____________ЃЌФуЕФРэгЩЪЧ________________________________.
(3)Ьхг§РЯЪІМЦЛЎИљОн2018ФъЕФЭГМЦЪ§ОнАВХХ75ЗжвдЯТЕФЭЌбЇВЮМгЬхжЪМгЧПбЕСЗЯюФПЃЌдђШЋФъМЖдМга________УћЭЌбЇВЮМгДЫЯюФП.