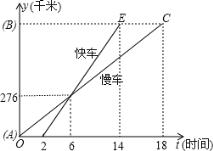
题目内容
【题目】我市某高科技公司生产一种矩形新型材料板,其长宽之比为 3∶2,每张材料板的成本 c与它的面积成正比例。每张材料板的销售价格 y与其宽 x 之间满足我们学习过的某种函数关系(即一次函数、反比例函数和二次函数关系中的一种),下表记录了该工厂生产、销售该材料板一些数据:
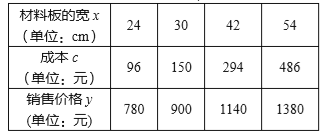
(1)求一张材料板的销售格 y 其宽 x 之间的函数关系式 (不必写出自变的取值范围)
(2)若一张材料板的利润 w 为销售价格 y与成本 c 的差
①请直接写出一张材料板的利润 w 其宽 x 之间的函数关系 (不必写出自变的取值范围)
②当材料板的宽为多少时,一张材料板的利润最大,最大利润是多少?
【答案】(1)![]() ;(2) ①
;(2) ① ![]() ;②当宽为60cm时,利润最大 ,最大利润为900元.
;②当宽为60cm时,利润最大 ,最大利润为900元.
【解析】
(1)根据图表可知所有点在一条直线上,故是一次函数,然后用待定系数法求出解析式并验证;
(2)①因为长宽之比为3:2,当宽为x时,则长为1.5x,根据矩形的面积公式可得x和y的关系进而得到c和x的关系,所以一张材料板的利润w与其宽x之间的函数关系可求出;②利用①中的函数性质即可求出当材料板的宽为多少时,一张材料板的利润最大,以及最大利润是多少.
解:(1)根据表中的数据判断,销售价格y于宽x之间的函数关系是一次函数,设其解析式为y=kx+b,
则24k+b=780,30k+b=900,
解得:k=20,b=300,
将x=42,y=1140和x=54,y=1380代入检验,满足条件
所以其解析式为y=20x+300;
(2)①∵矩形材料板,其长宽之比为3:2,
∴当宽为x时,则长为1.5x,
c=1.5kx2;k=![]() ,
,
即c=![]() x2,
x2,
∴w=![]() x2+20x+300;
x2+20x+300;
②由①可知:w=![]() x2+20x+300=
x2+20x+300=![]() (x60)2+900,
(x60)2+900,
∴当材料板的宽为60cm时,一张材料板的利润最大,最大利润是900元.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.