Question

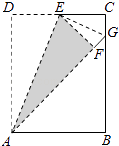
【题目】如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若 = ，则 =用含k的代数式表示）．

Answer 1

【答案】
【解析】解：∵点E是边CD的中点， ∴DE=CE，
∵将△ADE沿AE折叠后得到△AFE，
∴DE=EF，AF=AD，∠AFE=∠D=90°，
∴CE=EF，
连接EG，
在Rt△ECG和Rt△EFG中，
，
∴Rt△ECG≌Rt△EFG（HL），
∴CG=FG，
设CG=a，
∵ = ，
∴GB=ka，
∴BC=CG+BG=a+ka=a（k+1），
在矩形ABCD中，AD=BC=a（k+1），
∴AF=a（k+1），
AG=AF+FG=a（k+1）+a=a（k+2），
在Rt△ABG中，AB= = =2a ，
∴ = = ．
所以答案是： ．

【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．