题目内容
【题目】已知：二次函数y=ax2+bx+c， y与x的一些对应值如下表：
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
（1）根据表格中的数据，确定二次函数解析式为_________________；
（2）填齐表格中空白处的对应值并利用上表，用五点作图法，画出二次函数y=ax2+bx+c的图象．（不必重新列表）
（3）当 1 < x ≤4时，y的取值范围是_________________；
【答案】(1) y= x2-4x+3;(2)图象见解析；（3）-1≤y≤3
【解析】（1）把表中三组对应值代入y=ax2+bx+c中得关于a、b、c的方程组，然后解方程组求出a、b、c即可得到抛物线解析式，然后计算自变量为-1、1、3所对应的函数值；
（2）先把解析式配成顶点式，然后利用描点法画函数图象，再利用函数图象写出1＜x≤4时所对应y的取值范围．
(1)将点（0，3），（2，-1），（4，3）代入y=ax2+bx+c中，
，解得：
，
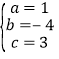∴二次函数解析式为
，
当x=-1时，y=8；当x=1时，y=0；当x=3时，y=0.
（2）如图，
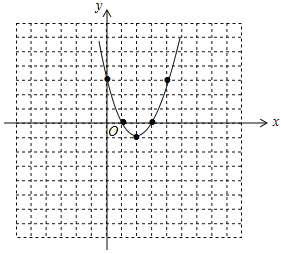
，抛物线的顶点坐标为（2，-1），
当
时，y的取值范围是
.
练习册系列答案
相关题目
【题目】一辆出租车从
地出发，在一条东西走向的街道上往返，每次行驶的路程（记向东为正）记录如下（
且
，单位：km）
第一次 | 第二次 | 第三次 | 第四次 |
|
|
| 2（9-x） |
（1）求经过连续
次行驶后，这辆出租车所在的位置；
（2）这辆出租车一共行驶了多少路程？
