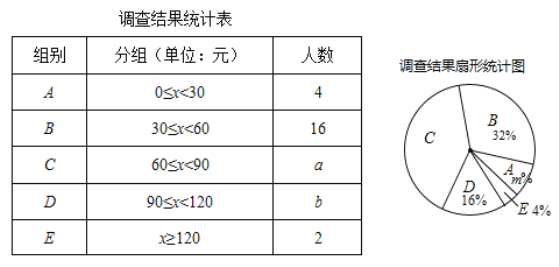
题目内容
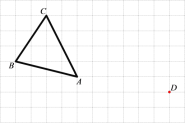
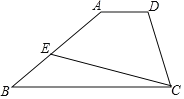
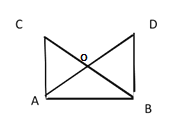
【题目】如图，海岸上有 A,B 两个观测点，点 B 在点 A 的正东方，海岛 C 在观测点 A 的正北方， 海岛 D 在观测点 B 的正北方。如果从观测点 A 看海岛 C，D 的视角∠CAD 与从观测点 B 海岛 C，D 的视角∠CBD 相等，那么海岛 C,D 到观测点 A,B 所在海岸的距离 CA,DB 相等，请说明理由。
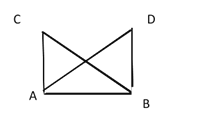
【答案】相等，理由见解析
【解析】
由方位可以得出∠CAB=∠DBA，而已知视角∠CAD=视角∠CBD，公共边AB=BA，容易得出△ABC≌△BAD，所以AC=BD．
相等，
理由：
∵∠CAD=∠CBD,∠COA=∠DOB(对顶角)，
∴由内角和定理，得∠C=∠D，
又∵∠CAB=∠DBA=90，
在△CAB和△DBA中，
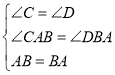
∴△CAB≌△DBA(AAS)，
∴CA=DB，
∴海岛C. D到观测点A. B所在海岸的距离相等.
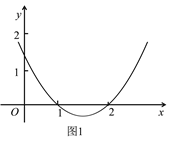
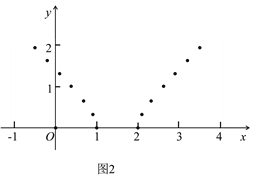
【题目】已知：二次函数y=ax2+bx+c， y与x的一些对应值如下表：
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
（1）根据表格中的数据，确定二次函数解析式为_________________；
（2）填齐表格中空白处的对应值并利用上表，用五点作图法，画出二次函数y=ax2+bx+c的图象．（不必重新列表）
（3）当 1 < x ≤4时，y的取值范围是_________________；
【题目】
年春节期间，某物业公司组织两个小区的部分居民去旅游，已知某景点的门票价格如下表：
购票人数 |
|
|
|
每人门票价 |
|
|
|
小区①的人数少于
人，小区②的人数多于人且少于
人，如果两小区单独购票，则一共支付
元；如果两小区联合起来作为一个团体购票，因为人数超过人，只需花费
元请问：
（1）两个小区各有多少人？
（2）团体购票与单独购票相比较，两个小区各节省了多少钱？
（3）若小区①单独购票，请为小区①设计一种最省钱的购买方案，并计算能省多少元钱？
