ЬтФПФкШн
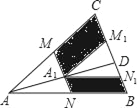
ЁОЬтФПЁПвбжЊAЁЂBЁЂCЮЊЪ§жсЩЯШ§ЕуЃЌШєЕуCЕНЕуAЕФОрРыЪЧЕуCЕНЕуBЕФОрРыЕФ2БЖЃЌдђГЦЕуCЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЌР§ШчЭМ1жаЃЌЕуAБэЪОЕФЪ§ЮЊЉ1ЃЌЕуBБэЪОЕФЪ§ЮЊ2ЃЌБэЪО1ЕФЕуCЕНЕуAЕФОрРыЮЊ2ЃЌЕНЕуBЕФОрРыЮЊ1ЃЌдђЕуCЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЌЕЋВЛЪЧЃЈBЃЌAЃЉЕФЦцвьЕуЃЎ
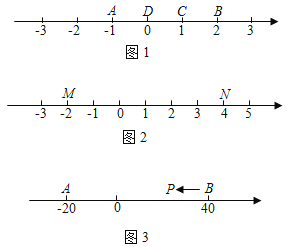
ЃЈ1ЃЉдкЭМ1жаЃЌжБНгЫЕГіЕуDЪЧЃЈAЃЌBЃЉЛЙЪЧЃЈBЃЌCЃЉЕФЦцвьЕуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЪ§жсЩЯMЁЂNСНЕуБэЪОЕФЪ§ЗжБ№ЮЊЉ2КЭ4ЃЌ
ЂйШєЃЈMЃЌNЃЉЕФЦцвьЕуKдкMЁЂNСНЕужЎМфЃЌдђKЕуБэЪОЕФЪ§ЪЧЁЁ ЁЁЃЛ
ЂкШєЃЈMЃЌNЃЉЕФЦцвьЕуKдкЕуNЕФгвВрЃЌЧыЧѓГіKЕуБэЪОЕФЪ§ЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌAЁЂBдкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊЉ20КЭ40ЃЌЯжгавЛЕуPДгЕуBГіЗЂЃЌЯђзѓдЫЖЏЃЎШєЕуPЕНДяЕуAЭЃжЙЃЌдђЕБЕуPБэЪОЕФЪ§ЮЊЖрЩйЪБЃЌPЁЂAЁЂBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЃП
ЁОД№АИЁПЃЈ1ЃЉЕуDЪЧЃЈBЃЌCЃЉЕФЦцвьЕуЃЌВЛЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЛЃЈ2ЃЉЂй2ЃЛЂк10ЃЛЃЈ3ЃЉЕБЕуPБэЪОЕФЪ§ЪЧ0Лђ10Лђ20ЪБЃЌPЁЂAЁЂBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАЦцвьЕуЁБЕФИХФюНтД№ЃЛ
ЃЈ2ЃЉЂйЩшЦцвьЕуБэЪОЕФЪ§ЮЊaЃЌИљОнЁАЦцвьЕуЁБЕФЖЈвхСаГіЗНГЬВЂНтД№ЃЛ
ЂкЪзЯШЩшKБэЪОЕФЪ§ЮЊxЃЌИљОнЃЈ1ЃЉЕФЖЈвхМДПЩЧѓГіxЕФжЕЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЬжТлЫЕУївЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЃЌСаГіЗНГЬМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЕуDЕНЕуAЕФОрРыЮЊ1ЃЌЕуDЕНЕуCЕФОрРыЮЊ1ЃЌЕНЕуBЕФОрРыЮЊ2ЃЌ
ЁрЕуDЪЧЃЈBЃЌCЃЉЕФЦцвьЕуЃЌВЛЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЛ
ЃЈ2ЃЉЂйЩшЦцвьЕуKБэЪОЕФЪ§ЮЊaЃЌ
дђгЩЬтвтЃЌЕУaЃЈ2ЃЉЃН2ЃЈ4aЃЉЃЎ
НтЕУaЃН2ЃЎ
ЁрKЕуБэЪОЕФЪ§ЪЧ2ЃЛ
ЂкЃЈMЃЌNЃЉЕФЦцвьЕуKдкЕуNЕФгвВрЃЌЩшKЕуБэЪОЕФЪ§ЮЊxЃЌ
дђгЩЬтвтЕУЃЌ
xЉЃЈЉ2ЃЉЃН2ЃЈxЉ4ЃЉ
НтЕУxЃН10
ЁрШєЃЈMЃЌNЃЉЕФЦцвьЕуKдкЕуNЕФгвВрЃЌKЕуБэЪОЕФЪ§ЮЊ10ЃЛ
ЃЈ3ЃЉЩшЕуPБэЪОЕФЪ§ЮЊyЃЌ
ЕБЕуPЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЪБЃЌ
дђгаy+20ЃН2ЃЈ40ЉyЃЉ
НтЕУyЃН20ЃЎ
ЕБЕуPЪЧЃЈBЃЌAЃЉЕФЦцвьЕуЪБЃЌ
дђга40ЉyЃН2ЃЈy+20ЃЉ
НтЕУyЃН0ЃЎ
ЕБЕуAЪЧЃЈBЃЌPЃЉЕФЦцвьЕуЪБЃЌ
дђга40+20ЃН2ЃЈy+20ЃЉ
НтЕУyЃН10ЃЎ
ЕБЕуBЪЧЃЈAЃЌPЃЉЕФЦцвьЕуЪБЃЌ
дђга40+20ЃН2ЃЈ40ЉyЃЉ
НтЕУyЃН10ЃЎ
ЁрЕБЕуPБэЪОЕФЪ§ЪЧ0Лђ10Лђ20ЪБЃЌPЁЂAЁЂBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЃЎ

 ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§y=ax2+bx+cЃЌ yгыxЕФвЛаЉЖдгІжЕШчЯТБэЃК
x | ЁЁ | 1 | 0 | 1 | 2 | 3 | 4 | ЁЁ |
ax2+bx+c | ЁЁ | 3 | 1 | 3 | ЁЁ |
ЃЈ1ЃЉИљОнБэИёжаЕФЪ§ОнЃЌШЗЖЈЖўДЮКЏЪ§НтЮіЪНЮЊ_________________ЃЛ
ЃЈ2ЃЉЬюЦыБэИёжаПеАзДІЕФЖдгІжЕВЂРћгУЩЯБэЃЌгУЮхЕузїЭМЗЈЃЌЛГіЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓЃЎЃЈВЛБижиаТСаБэЃЉ
ЃЈ3ЃЉЕБ 1 < x Ём4ЪБЃЌyЕФШЁжЕЗЖЮЇЪЧ_________________ЃЛ

ЁОЬтФПЁПЮЊСЫТњзубЇЩњЕФЮяжЪашЧѓЃЌЮвЪаФГжабЇЕНКьЦьГЌЪазМБИЙКНјМзЁЂввСНжжТЬЩЋДќзАЪГЦЗ.ЦфжаМзЁЂввСНжжТЬЩЋДќзАЪГЦЗЕФНјМлКЭЪлМлШчЯТБэЃК
Мз | вв | |
НјМлЃЈдЊ/ДќЃЉ |
|
|
ЪлМлЃЈдЊ/ДќЃЉ | 20 | 13 |
вбжЊЃКгУ2000дЊЙКНјМзжжДќзАЪГЦЗЕФЪ§СПгыгУ1600дЊЙКНјввжжДќзАЪГЦЗЕФЪ§СПЯрЭЌ.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвЊЪЙЙКНјЕФМзЁЂввСНжжТЬЩЋДќзАЪГЦЗЙВ800ДќЕФзмРћШѓЃЈРћШѓ=ЪлМл-НјМлЃЉВЛЩйгк5200дЊЃЌЧвВЛГЌ5280дЊЃЌЮЪИУКьЦьГЌЪагаМИжжНјЛѕЗНАИЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌИУКьЦьГЌЪазМБИЖдМзжжДќзАЪГЦЗНјаагХЛнДйЯњЛюЖЏЃЌОіЖЈЖдМзжжДќзАЪГЦЗУПДќгХЛн![]() дЊГіЪлЃЌввжжДќзАЪГЦЗМлИёВЛБф.ФЧУДИУКьЦьГЌЪавЊЛёЕУзюДѓРћШѓгІШчКЮНјЛѕЃП
дЊГіЪлЃЌввжжДќзАЪГЦЗМлИёВЛБф.ФЧУДИУКьЦьГЌЪавЊЛёЕУзюДѓРћШѓгІШчКЮНјЛѕЃП