题目内容
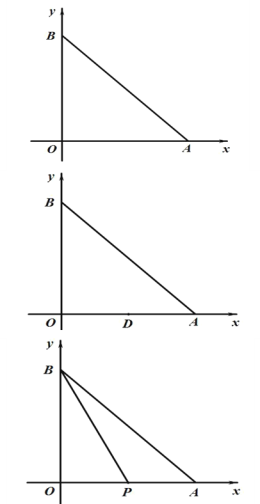
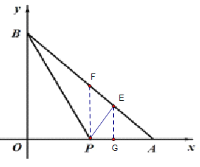
【题目】已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),AB=6![]() ,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
(1)求点 B 的坐标;
(2)设点 P 的运动时间为点 t 秒,△BDP 的面积为 S,求 S 与 t 的函数关系式;
(3)当点 P 与点 D 重合时,连接 BP,点 E 在线段 AB 上,连接 PE,当∠BPE=2∠OBP 时, 求点 E 的坐标.
【答案】(1)B(0,6);(2)S=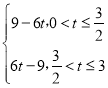 ;(3)E(4,2)
;(3)E(4,2)
【解析】
(1)在Rt△AOB中,利用勾股定理可求得OB的长,从而得到点B的坐标;
(2)存在2种情况,一种是点P在点D的左侧,一种是在右侧,求△PBD的面积,高始终是OB不变,仅需表示出PD的长即可;
(3)如下图,作∠BPE的角平分线PF,根据角之间的关系,可得到PF∥OB,从而推导出△PEG∽△PBO,最后利用相似比的关系求得线段的长度,从而得到E的坐标.
(1)∵A(6,0),AB=6![]() ,△AOB是直角三角形
,△AOB是直角三角形
∴在Rt△AOB中,OB=![]()
∴B(0,6)
(2)情况一:如下图,点P在点D的左侧,即![]() 时
时
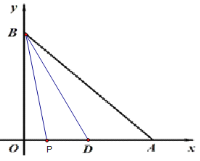
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=3-2t
∴S=![]()
情况二:如下图,点P在点D的右侧,即![]() 时
时
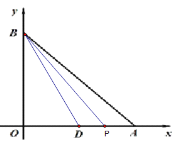
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=2t-3
∴S=![]()
综上得:S=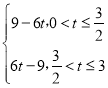
(3)如下图,PF是∠PBE的角平分线,交AB于点F,过点E作x轴的垂线,交x轴于点G
∵OA=6,OB=6,AB=6![]()
∴△OBA是等腰直角三角形,∠A=45°
∴△GEA是等腰直角三角形
设PG=x,则AG=3-x
∴EG=AG=3-x
∵PF是∠BPE的角平分线,∴∠BPF=∠FPE
∵∠BPE=2∠OBP
∴∠OBP=∠BPF=∠FPE
∴PF∥OB,∴PF⊥OA
∴∠FPE+∠EPG=90°
∵∠OBP+∠BPO=90°,∴∠EPG=∠BPO
∵∠EGP=∠BOP
∴△PEG∽△PBO
∴![]() ,即
,即![]() ,解得:x=1
,解得:x=1
∴PG=1,GE=2
∴E(4,2)

【题目】已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.
(1)写出y关于x的函数关系式 ;x的取值范围是 .
(2)列表,得
x | … | 1 | 2 | 3 | 4 | … |
y | … |
|
|
|
| … |
在给出的坐标系中描点并连线;
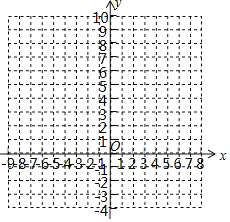
(3)如果A(x1,y1),B(x2,y2)是图象上的两个点,且x1>x2>0,试判断y1,y2的大小.