题目内容
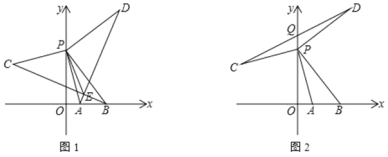
【题目】已知如图,在平面直角坐标系中,点 B(m,0)、A(n,0)分别是 x 轴轴上两点, 且满足多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,点 P(0,h)是 y 轴正半轴上的动点
(1)求三角形△ABP 的面积(用含 h 的代数式表示)
(2)过点 P 作 DP⊥PB,CP⊥PA,且 PD=PB,PC=AP
① 连接 AD、BC 相交于点 E,再连 PE,求∠BEP 的度数
② 连 CD 与 y 轴相交于点 Q,当动点 P 在 y 轴正半轴上运动时,线段 PQ 的长度变不变?如果不变,请求出其值;如果变化,请求出其变化范围
【答案】(1) m=3,n=1; ![]() =h;(2) ∠BEP=135
=h;(2) ∠BEP=135![]() ;(3)PQ=1.
;(3)PQ=1.
【解析】
(1)由多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,可求得m、n的值,可求得三角形△ABP 的面积;
(2)①又DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,可证△BPC≌△DPA,可得∠C=∠A,在CB的线段上取F点,使得CF=AE,连接PF,可得△CPF≌△APE,可得PF=PE, ∠CPF= ∠APE,可得△PEF为等腰直角三角形,可求出∠BEP 的度数;
②由DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,A点坐标为(1,0),B点坐标为(3,0),P点坐标(0,h),由旋转的特性,可得C点坐标为(-h,h-1),D点坐标(h,h+3),
可得CD的解析式,可得Q点坐标及PQ的长.
解:(1) ![]() 多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,
多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,
![]() 展开得:
展开得:![]()
=![]()
![]() m-3=0,
m-3=0,![]() =0,
=0,
解得:m=3,n=1,
![]()
![]() =
=![]() AB
AB![]() OP=
OP=![]()
![]() 2
2![]() h=h;
h=h;
(2)①如图: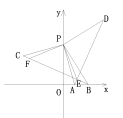
由题意得:DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,
又![]() ∠APB=∠APB,
∠APB=∠APB,![]() ∠APC+∠APB=∠BPD+∠APB
∠APC+∠APB=∠BPD+∠APB
![]() ∠APC=∠BPD,
∠APC=∠BPD,
在△BPC与△DPA中,
PD=PB,PC=AP,∠APC=∠BPD
![]() △BPC≌△DPA,
△BPC≌△DPA,![]() ∠C=∠A
∠C=∠A
在CB的线段上取F点,使得CF=AE,连接PF,
在△CPF与△APE中,
∠C=∠A,CF=AE,PC=AP,
![]() △CPF≌△APE,
△CPF≌△APE,![]() PF=PE, ∠CPF= ∠APE,
PF=PE, ∠CPF= ∠APE,
![]() ∠FPE=90
∠FPE=90![]() ,又PF=PE,
,又PF=PE,
![]() △PEF为等腰直角三角形,
△PEF为等腰直角三角形,
![]() ∠PEF=45
∠PEF=45![]() ,
,
![]() ∠BEP=135
∠BEP=135![]() .
.
②由DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,A点坐标为(1,0),B点坐标为(3,0),P点坐标(0,h),由旋转的特性,可得C点坐标为(-h,h-1),D点坐标(h,h+3),
设CD的解析式为y=kx+b,代入CD两点坐标,可得CD解析式为:![]() ,
,
故Q点坐标为(0,h+1),
![]() P点坐标为(0,h),
P点坐标为(0,h),
![]() PQ的长为定值为:h+1-h=1.
PQ的长为定值为:h+1-h=1.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案