题目内容
【题目】如图：抛物线y=ax2+bx+c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC+OD， 
（1）求抛物线的解析式；
（2）设点P（x，y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，写出自变量x的取值范围，并求当x取多少时，S的值最大，最大是多少？
【答案】
（1）解：（1）∵OC=4，OD=2，
∴DM=6，
∴点M（2，6），
设y=a（x﹣2）2+6，代入（0，4）得：a=﹣ 
，
∴该抛物线解析式为y=﹣ （x﹣2）2+6；
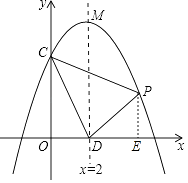
（2）（2）设点P（x，﹣ （x﹣2）2+6），即（x，﹣ x2+2x+4），x＞0，
过点P作x轴的垂线，交x轴于点E，
则PE=﹣ x2+2x+4，DE=x﹣2，
S= x（﹣ x2+2x+4+4）﹣ ×2×4﹣ （x﹣2）（﹣ x2+2x+4），
即S=﹣ x2+4x=﹣ （x﹣4）2+8，
∴当x=4时，S有最大值为8．
【解析】（1）由OC与OD的长，求出MD的长，确定出M坐标，设y=a（x﹣2）2+6，把C坐标代入求出a的值，即可确定出抛物线解析式；（2）由抛物线解析式设出P坐标，过点P做x轴的垂线，交x轴于点E，利用表示出的点P的坐标确定出线段PE、DE的长，用梯形OCPE的面积减去直角三角形OCD的面积和直角三角形PDE的面积，进而得出S与x的函数解析式，利用二次函数性质求出S最大值时x的值即可．
练习册系列答案
相关题目
