题目内容
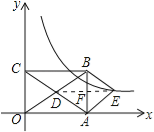
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.

【答案】(1)见解析;(2)y=![]() .
.
【解析】试题分析:(1)先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,即可证出四边形AEBD是菱形;
(2)连接DE,交AB于F,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;设经过点E的反比例函数解析式为:y=![]() ,把点E坐标代入求出k的值即可.
,把点E坐标代入求出k的值即可.
(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=![]() OA=
OA=![]() ,AF=
,AF=![]() AB=1,3+
AB=1,3+![]() =
=![]() ,
,
∴点E坐标为:(![]() ,1),
,1),
设经过点E的反比例函数解析式为:y=![]() ,
,
把点E(![]() ,1)代入得:k=
,1)代入得:k=![]() ,
,
∴经过点E的反比例函数解析式为:y=![]() .
.

练习册系列答案
相关题目