题目内容
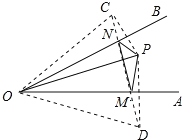
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
【答案】B
【解析】
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=DM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB![]() ∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示.
∵点P关于OA的对称点为D,关于OB的对称点为C,∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB,∴OC=OP=OD,∠AOB![]() ∠COD.
∠COD.
∵△PMN周长的最小值是6cm,∴PM+PN+MN=6,∴DM+CN+MN=6,即CD=6=OP,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°.
故选B.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】为保护和改善环境,发展新经济,国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展,为响应号召,某市某汽车专卖店销售A,B两种型号的新能源汽车共25辆,这两种型号的新能源汽车的进价、售价如下表:
进价 | 售价 | |
A型 | 10 |
|
B型 | 15 |
|
![]() 如何进货,进货款恰好为325万元?
如何进货,进货款恰好为325万元?
![]() 如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的
如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?