题目内容
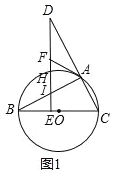
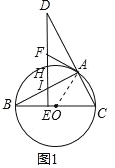
【题目】如图1,BC是![]() 的直径,点A在
的直径,点A在![]() 上,点D在CA的延长线上,
上,点D在CA的延长线上,![]() ,垂足为点E,DE与
,垂足为点E,DE与![]() 相交于点H,与AB相交于点
相交于点H,与AB相交于点![]() 过点A作
过点A作![]() ,与DE相交于点F.
,与DE相交于点F.
![]() 求证:AF为
求证:AF为![]() 的切线;
的切线;
![]() 当
当![]() ,且
,且![]() 时,求:
时,求:![]() 的值;
的值;
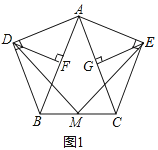
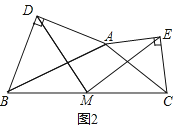
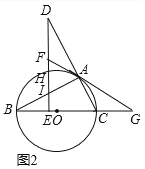
![]() 如图2,在
如图2,在![]() 的条件下,延长FA,BC相交于点G,若
的条件下,延长FA,BC相交于点G,若![]() ,求线段EH的长.
,求线段EH的长.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
![]() 欲证明AF是切线,只要证明
欲证明AF是切线,只要证明![]() 即可;
即可;
![]() 首先证明
首先证明![]() ,推出
,推出![]() ,推出
,推出![]() ,由
,由![]() ,推出
,推出![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,推出
,推出![]() ,在
,在![]() 中,
中,![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
![]() 只要证明
只要证明![]() ∽
∽![]() ,可得
,可得![]() ,由
,由![]() ,推出
,推出![]() ,
,![]() ,
,![]() ,由
,由![]() ,推出
,推出![]() ,可得
,可得![]() ,
,![]() ,再证明
,再证明![]() ∽
∽![]() ,可得
,可得![]() ,即可解决问题;
,即可解决问题;
![]() 证明:如图1中,连接OA.
证明:如图1中,连接OA.
![]() 是直径,
是直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 是
是![]() 的切线.
的切线.
![]() 解:如图2中,
解:如图2中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
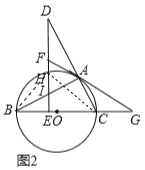
![]() 解:如图
解:如图![]() 中,连接CH、BH.
中,连接CH、BH.
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
可得![]() ,
,
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.