题目内容
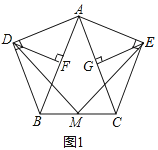
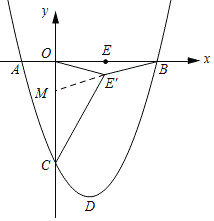
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
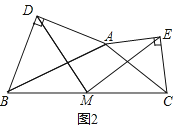
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
![]() 由抛物线的交点式可知抛物线的解析式为
由抛物线的交点式可知抛物线的解析式为![]() ,通过整理可得到抛物线的解析式,然后利用配方法可得到抛物线的定点坐标;
,通过整理可得到抛物线的解析式,然后利用配方法可得到抛物线的定点坐标;
![]() 过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点
过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点![]() 以
以![]() 为直径的
为直径的![]() 如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点
如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点![]() 了,以AB为直径作
了,以AB为直径作![]() ,作QD与
,作QD与![]() 相切,则
相切,则![]() ,过
,过![]() 作
作![]() ,先求得点
,先求得点![]() 的坐标,于是可求得l的解析式,由图形的对称性可知点
的坐标,于是可求得l的解析式,由图形的对称性可知点![]() 的坐标还可以是
的坐标还可以是![]() ,然后可求得另一种情况;
,然后可求得另一种情况;
![]() 取
取![]() 使
使![]() ,连接
,连接![]() ,接下来,证明
,接下来,证明![]() ∽
∽![]() ,从而可得到
,从而可得到![]() ,故此当
,故此当![]() 、
、![]() 、
、![]() 在一条直线上时,
在一条直线上时,![]() 有最小值,最后,依据勾股定理求得
有最小值,最后,依据勾股定理求得![]() 的长度即可.
的长度即可.
![]() 抛物线
抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,
两点,
![]() .
.
![]() ,
,
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() .
.
![]() 过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
以AB为直径的![]() 如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
如图所示:以AB为直径作![]() ,作QD与
,作QD与![]() 相切,则
相切,则![]() ,过Q作
,过Q作![]() .
.

![]() ,
,![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() 点Q的坐标为
点Q的坐标为![]() .
.
设l的解析式为![]() ,则
,则![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]() 直线l的解析式为
直线l的解析式为![]() .
.
由图形的对称性可知:当直线l经过点![]() 时,直线l与
时,直线l与![]() 相切,
相切,
则![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 直线l的解析式为
直线l的解析式为![]() .
.
综上所述,直线l的解析式为![]() 或
或![]() .
.
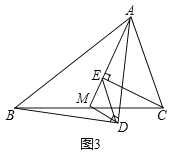
![]() 如图所示:取M使
如图所示:取M使![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ∽
∽![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() 当M、
当M、![]() 、B在一条直线上时,
、B在一条直线上时,![]() 有最小值,
有最小值,
![]() 的最小值
的最小值![]() .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.