题目内容
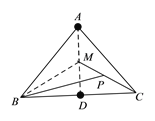
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
【答案】(1) ∠MPB=40°;(2) ∠BAC+∠ABP=120°.证明见解析
【解析】试题分析:(1)由AB=AC,∠BAC=80°,可求∠ABC=∠ACB=50°,又∠PBC=10°,∠ABP=2∠ACM,可求∠BCM=30°,由三角形外角的性质可求出结果;
(2)过点A作底边BC的中线AD,连接BM,由等腰三角形三线合一的性质可得∠CAM=∠BAM,从而可证△ABM≌△ACM.进而证明△ABM≌△PBM.可证出∠AMB=120°,进而得出结论.
试题解析:(1)∵ AB=AC,
∴∠ABC=∠ACB.
∵∠BAC=80°,
∴∠ABC=∠ACB=50°.
∵∠PBC=10°,
∴∠ABP=40°.
∵∠ABP=2∠ACM,
∴∠ACM=20°.
∴∠BCM=30°.
∴∠MPB=∠PBC+∠BCM= 40°;
(2)∠BAC+∠ABP=120°.
证明:过点A作底边BC的中线AD,
∵AB=AC,
∴AD是∠BAC的平分线.
∵点M在底边BC的中线上,
∴点M在∠BAC的平分线AD上.
即AM平分∠BAC.
∴∠CAM=∠BAM.
∴连接BM,又AM是公共边
△ABM≌△ACM.
∴∠ACM=∠ABM.
∠ABP=2∠ACM,
∴∠ABP=2∠ABM.
∴∠ABM=∠PBM.
∵BP=AC,
∴BP=AB.
∴△ABM≌△PBM.
∴∠AMB=∠PMB.
又∵△ABM≌△ACM,
∴∠AMB=∠AMC.
∴∠AMB=∠AMC=∠PMB.
∴∠AMB=120°.
∴∠BAM+∠ABM=60°.
∵∠BAC=2∠BAM,
∠ABP=2∠ABM,
∴∠BAC+∠ABP=120°.

 阅读快车系列答案
阅读快车系列答案